题目内容
16.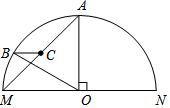 如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.
如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.求证:$\widehat{MB}$=$\frac{1}{3}$$\widehat{AM}$.
分析 先作出辅助线,延长BC交AO于点D.由C为AM的中点,BC∥MN,可得出CD为△AMO的中位线,即可得到AD,OD与AO的关系,从而得出OD=$\frac{1}{2}$BO,在Rt△BDO中,利用特殊三角形可得出∠OBD=30°,得∠BOM=30°,即可得出$\widehat{MB}$=$\frac{1}{3}$$\widehat{AM}$.
解答 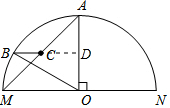 解:如图,延长BC交AO于点D.
解:如图,延长BC交AO于点D.
∵C为AM的中点,BC∥MN,
∴AD=OD=$\frac{1}{2}$AO,
∴OD=$\frac{1}{2}$BO,
∵OA⊥MN,
∴∠AOM=90°,
∴∠BDO=90°,
∴∠OBD=30°,
∴∠BOM=30°,
∴$\widehat{MB}$=$\frac{1}{3}$$\widehat{AM}$.
点评 本题主要考查了圆的综合题,解题的关键是正确作出辅助线,灵活运用含有30°的直角三角形的知识.

练习册系列答案
相关题目
6.一个食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正要做促销活动,购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为29元.
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
11.一次函数y=kx+3的自变量取值增加2,函数值就相应减少2,则k的值为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 4 |
8.(-1)2003+(-1)2004=( )
| A. | 0 | B. | -1 | C. | 1或者-1 | D. | 1 |
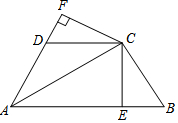 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.