题目内容
4.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
请用上面的知识解答下面的问题:
(1)数轴上表示1和5的两点之间的距离是4,数轴上表示-2和-4的两点之间的距离是2,数轴上表示1和-3的两点之间的距离是4;
(2)数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
(3)|x+1|+|x-2|取最小值是3.
分析 (1)依据数轴上A、B两点之间的距离AB=|a-b|进行计算即可;
(2)数轴上A、B两点之间的距离AB=|a-b|列出方程求解即可;
(3)|x+1|+|x-2|取最小值表示数轴上某点到-1和2的距离之和,从而可求得最小值.
解答 解:(1)数轴上表示1和5的两点之间的距离是=|5-1|=4;
数轴上表示-2和-4的两点之间的距离=|-2-(-4)|=2;
数轴上表示1和-3的两点之间的距离是=|-3-1|=4;
故答案为:4;2;4;
(2)数轴上表示x和-1的两点A和B之间的距离=|x-(-1)|=|x+1|;
∵|AB|=2,
∴x+1=±2.
解得:x=1或x=-3.
故答案为:|x+1|;1或-3;
(3)|x+1|+|x-2|表示数轴上某点到-1和2的距离之和.
∴当-1≤x≤2时,|x+1|+|x-2|有最小值,最小值为3.
故答案为:3.
点评 本题主要考查的是绝对值、数轴的认识,理解绝对值的几何意义是解题的关键.

练习册系列答案
相关题目
12.函数y=x2+3x-4的图象与y轴的交点坐标是( )
| A. | (2,0) | B. | (-2,0) | C. | (0,4) | D. | (0,-4) |
9.已知(x2+y2+1)(x2+y2+3)=8,则x2+y2的值为( )
| A. | -5或1 | B. | 5或-1 | C. | 5 | D. | 1 |
16.一个长方形的周长为6a+8b,若一边长为2a+b,则它的另一边长为( )
| A. | 4a+5b | B. | a+b | C. | a+3b | D. | a+7b |
13.若a>0,b<0,且|a|<|b|,则a+b等于( )
| A. | -(|b|-|a|) | B. | -(|a|-|b|) | C. | -(|a|+|b|) | D. | |a|+|b| |

 .
. 表示正,
表示正, .
. 表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):-[2×(-6)+3×(-4)]=24;[2-3×(-6)]-(-4)=24;;
表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):-[2×(-6)+3×(-4)]=24;[2-3×(-6)]-(-4)=24;;
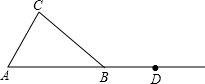 如图,在△ABC中,AB=BC,点D在AB的延长线上.
如图,在△ABC中,AB=BC,点D在AB的延长线上.