题目内容
14.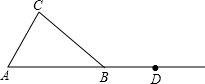 如图,在△ABC中,AB=BC,点D在AB的延长线上.
如图,在△ABC中,AB=BC,点D在AB的延长线上.(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F.
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由.
分析 (1)先作∠CBD的平分线BM,再作线段BC的垂直平分线得到BC的中点E,然后连结AE并延长交BM于F;
(2)先证明∠CBD=∠BAC,再证明△ACE≌△FEB得到AE=FE,然后利用对角线互相平分的四边形为平行四边形可判断四边形ABFC为平行四边形.
解答 解:(1)如图,BM、AF为所作;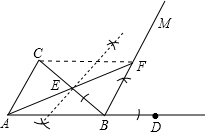
(2)四边形ABFC为平行四边形.理由如下:
∵BM平分∠CBD,
∴∠DBM=∠CBM,
∵BA=BC,
∴∠BAC=∠BCA,
而∠CBD=∠BAC+∠BCA,
∴∠CBD=∠BAC,
在△ACE和△FEB中,
$\left\{\begin{array}{l}{∠ACE=∠FBE}\\{CE=BE}\\{∠AEC=∠FEB}\end{array}\right.$,
∴△ACE≌△FEB,
∴AE=FE,
∵CE=BE,
∴四边形ABFC为平行四边形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的判定.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
2.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 47.8元 |
9.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么当自变量x取m-1时,下列结论中正确的是( )
| A. | m-1的函数值小于0 | B. | m-1的函数值大于0 | ||
| C. | m-1的函数值等于0 | D. | m-1的函数值与0的大小关系不确定 |
19.若关于x的一元一次不等式组$\left\{\begin{array}{l}{2x-m≤0}\\{-x<3}\end{array}\right.$有解,则m的取值范围为( )
| A. | m<-6 | B. | m≤-6 | C. | m>-6 | D. | m≥-6 |
3.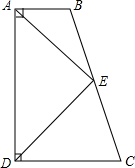 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )
 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
