题目内容
已知α,β是方程x2-2x-4=0的两实根,则α3+8β+6的值为 .
考点:根与系数的关系,一元二次方程的解
专题:计算题
分析:先根据一元二次方程的解的定义得到α2=2α+4,再用α表示α3,则运算可化简为8(α+β)+14,然后利用根与系数的关系求解.
解答:解:∵α方程x2-2x-4=0的实根,
∴α2-2α-4=0,即α2=2α+4,
∴α3=2α2+4α=2(2α+4)+4α=8α+8,
∴原式=8α+8+8β+6
=8(α+β)+14,
∵α,β是方程x2-2x-4=0的两实根,
∴α+β=2,
∴原式=8×2+14=30.
故答案为30.
∴α2-2α-4=0,即α2=2α+4,
∴α3=2α2+4α=2(2α+4)+4α=8α+8,
∴原式=8α+8+8β+6
=8(α+β)+14,
∵α,β是方程x2-2x-4=0的两实根,
∴α+β=2,
∴原式=8×2+14=30.
故答案为30.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程的解.
| b |
| a |
| c |
| a |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
a=
,b=
,则a+b-ab的值是( )
| 1 | ||
2-
|
| 1 | ||
2+
|
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、2
|
已知a,b为实数,(a2+b2)2-(a2+b2)-6=0,则代数式a2+b2的值为( )
| A、2 | B、3 | C、-2 | D、3或-2 |
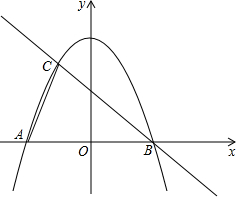 如图,抛物线y=
如图,抛物线y= 如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a-b|+
如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a-b|+ 如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,已知⊙O的半径为5cm,AE=3cm,BF=5cm,求CD的长.
如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,已知⊙O的半径为5cm,AE=3cm,BF=5cm,求CD的长.