题目内容
若a与b是关于x的方程x2+2x-2012=0的两根,则a2+3a+b= .
考点:根与系数的关系,一元二次方程的解
专题:计算题
分析:先根据一元二次方程的解得到a2+2a-2012=0,则a2+2a=2012,所以原式可化简为a+b+2012,然后利用根与系数的关系求解.
解答:解:∵a是关于x的方程x2+2x-2012=0的根,
∴a2+2a-2012=0,
∴a2+2a=2012,
∴原式=a+b+2012,
∵a与b是关于x的方程x2+2x-2012=0的两根,
∴a+b=-2,
∴原式=-2+2012=2010.
故答案为2010.
∴a2+2a-2012=0,
∴a2+2a=2012,
∴原式=a+b+2012,
∵a与b是关于x的方程x2+2x-2012=0的两根,
∴a+b=-2,
∴原式=-2+2012=2010.
故答案为2010.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程的解.
| b |
| a |
| c |
| a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
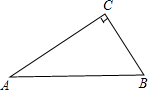 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.
 如图,EF∥AD,AD∥BC,∠1=∠2,∠DAC=120°,∠3=20°.求∠FEC的度数.
如图,EF∥AD,AD∥BC,∠1=∠2,∠DAC=120°,∠3=20°.求∠FEC的度数.