题目内容
12. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.
分析 根据正方形的性质,可得边相等,角相等,根据扇形BAC与扇形CBD的弧交于点E,可得△BCE的形状,根据图形的割补,可得阴影的面积是扇形,根据扇形的面积公式,可得答案.
解答 解:正方形ABCD中,
∴∠DCB=90°,DC=AB=6cm.
扇形BAC与扇形CBD的弧交于点E,
∴△BCE是等边三角形,∠ECB=60°,.
∴∠DCE=∠DCB-∠ECB=30°.
根据图形的割补,可得阴影的面积是扇形DCE,
S扇形DCE=π×62×$\frac{30}{360}$=3π,
故答案为3π.
点评 本题主要考查了正方形的性质,扇形的面积,灵活应用图形的割补是解题关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.式子$\frac{1}{{\sqrt{x-1}}}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≠1 | C. | x<1 | D. | x>1 |
20.小红有4双完全相同的手套,都是左、右手不能换戴的,其中有两双是妈妈送的,一双是姑姑送的,另一双是同学送的,小红在这4双混放在一起的手套中任取两只,恰好是同学送的那双的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{16}$ |
7.2014年柳州市参加初中毕业学业(升学)统一考试的学生人数约为34000人,将34000用科学记数法表示应为( )
| A. | 34×103 | B. | 3.4×104 | C. | 3.4×105 | D. | 0.34×105 |
17. 如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )
如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )
 如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )
如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |

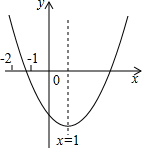 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论: