题目内容
2.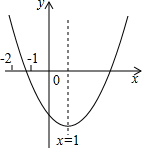 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③8a+c>0;④a+3b+c>0.
其中,正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①首先根据抛物线开口向上,可得a>0;再根据对称轴在y轴的右边,判断出b<0;然后根据二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的负半轴,可得c<0,所以abc>0,据此判断即可.
②根据抛物线的对称轴x=-$\frac{b}{2a}=1$,可得b+2a=0,据此判断即可.
③首先根据抛物线的对称轴是x=1,抛物线与x轴的一个交点-2<x1<-1,可得抛物线与x轴的另一个交点3<x2<4;然后根据x=4时,y>0,判断出8a+c>0即可.
④根据b+2a=0,可得b=-2a,所以a+3b+c=a+3×(-2a)+c=-5a+c<0,据此判断即可.
解答 解:∵抛物线开口向上,
∴a>0;
∵对称轴在y轴的右边,
∴b<0;
∵二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的负半轴,
∴c<0,
∴abc>0,
∴结论①正确;
∵抛物线的对称轴x=-$\frac{b}{2a}=1$,
∴b+2a=0,
∴结论②正确;
∵抛物线的对称轴是x=1,抛物线与x轴的一个交点-2<x1<-1,
∴抛物线与x轴的另一个交点3<x2<4;
∴x=4时,y>0,
∴16a+4b+c>0,
∵b+2a=0,
∴b=-2a,
∴8a+c>0,
∴结论③正确;
∵b+2a=0,
∴b=-2a,
∴a+3b+c=a+3×(-2a)+c=-5a+c<0,
∴结论④不正确.
综上,可得正确结论的个数是3个:①②③.
故选:C.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≠4 |
| A. | x4-x3=x | B. | x2x3=x6 | C. | x5÷x3=x2 | D. | (x2)3=x5 |
 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.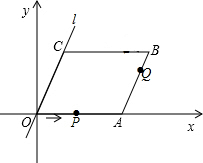 如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.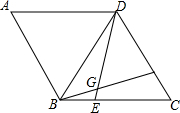 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.