题目内容
20.小红有4双完全相同的手套,都是左、右手不能换戴的,其中有两双是妈妈送的,一双是姑姑送的,另一双是同学送的,小红在这4双混放在一起的手套中任取两只,恰好是同学送的那双的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{16}$ |
分析 首先分别用A,a,B,b表示妈妈送的两双,用C,c表示姑姑送的一双,用D,d表示同学送的另一双;然后根据题意列出表格,再由表格求得所有等可能的结果与恰好是同学送的那双的情况,然后利用概率公式求解即可求得答案.
解答 解:分别用A,a,B,b表示妈妈送的两双,用C,c表示姑姑送的一双,用D,d表示同学送的另一双;
列表得:
| d | Ad | ab | Bd | bc | Cd | cd | Dd | - |
| D | AD | aB | BD | bD | CD | cD | - | dD |
| c | Ac | ac | Bc | bc | Cc | - | Dc | dc |
| C | AC | aC | BC | bC | - | cC | DC | dC |
| b | Ab | ab | Bb | - | Cb | cb | Db | db |
| B | AB | aB | - | bB | CB | cB | DB | dB |
| a | Aa | - | Ba | ba | Ca | ca | Da | da |
| A | - | aA | BA | bA | CA | cA | DA | dA |
| A | a | B | b | C | c | D | d |
∴恰好是同学送的那双的概率为:$\frac{2}{56}$=$\frac{1}{28}$.
故选C.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.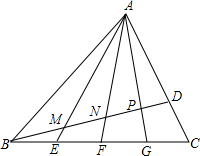 如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
 如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
11.若代数式$\frac{(x-2)(x-1)}{|x|-1}$的值为0,则x的值是( )
| A. | 2或1 | B. | 2且1 | C. | 2 | D. | 1 |
15.山地自行车越来越受到人们的喜爱,某车行经营的A型车,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和B型车共60辆,且B型车的进货数量不超过A型车数量的2倍,如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如下表:
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和B型车共60辆,且B型车的进货数量不超过A型车数量的2倍,如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如下表:
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
9.如图是一组有规律的图案,第1个图案由4个▲组成,第2个图案由7个▲组成,第3个图案由10个▲组成,第4个图案由13个▲组成,…,则第n(n为正整数)个图案由( )个▲组成.
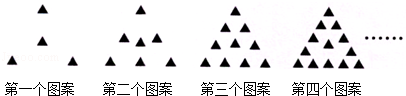

| A. | 4n+1 | B. | 3n+1 | C. | 4n-1 | D. | 3n-1 |
 过正方体中有公共顶点的三条棱的中点,切去一个三棱锥,形成如图的几何体,其展开图正确的是( )
过正方体中有公共顶点的三条棱的中点,切去一个三棱锥,形成如图的几何体,其展开图正确的是( )



 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.