题目内容
2.已知三角形三条边的长分别为3、x、9,化简:|3-$\frac{3}{4}$x|+|$\frac{1}{2}$x-3|=$\frac{5}{4}$x-3.分析 根据三角形的三边关系“任意两边之和>第三边,任意两边之差<第三边”,得到x的取值范围,再依此化简即可求解.
解答 解:根据三角形的三边关系,得
9-3<x<9+3,即6<x<12,
则|3-$\frac{3}{4}$x|+|$\frac{1}{2}$x-3|=$\frac{3}{4}$x+$\frac{1}{2}$x-3=$\frac{5}{4}$x-3.
故答案为:$\frac{5}{4}$x-3.
点评 本题主要考查了三角形的三边关系,任意两边之和>第三边,任意两边之差<第三边,比较简单.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
12.正方形ABCD内有一点E,且△ABE为等边三角形,则∠DCE为( )
| A. | 15° | B. | 18° | C. | 22.5° | D. | 30° |
10.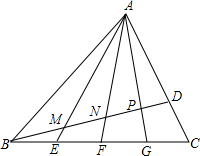 如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
 如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
如图,已知△ABC中,D为AC边上一点,CD=$\frac{1}{3}$AC,点E、F、G四等分边BC,连接AE、AF、AG分别与BD交于点M、N、P,则BM:BD=$\frac{1}{3}$.
11.若代数式$\frac{(x-2)(x-1)}{|x|-1}$的值为0,则x的值是( )
| A. | 2或1 | B. | 2且1 | C. | 2 | D. | 1 |

 如图所示,一只狗用铁链系在边长分别为6m和8m的矩形狗窝的一角上,铁链长10m,那么狗窝外面的狗活动范围的面积是80πm2.
如图所示,一只狗用铁链系在边长分别为6m和8m的矩形狗窝的一角上,铁链长10m,那么狗窝外面的狗活动范围的面积是80πm2. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为3πcm2.