题目内容
4.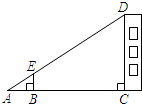 如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为10.5m.
如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为10.5m.
分析 先证明∴△ABE∽△ACD,则利用相似三角形的性质得$\frac{1.6}{1.6+12.4}$=$\frac{1.2}{CD}$,然后利用比例性质求出CD即可.
解答 解:∵EB∥CD,
∴△ABE∽△ACD,
∴$\frac{AB}{AC}$=$\frac{BE}{CD}$,即$\frac{1.6}{1.6+12.4}$=$\frac{1.2}{CD}$,
∴CD=10.5(米).
故答案为10.5.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.某校组织七年级学生到距离学校6km的科技馆去参观,小胖同学因事没能乘上学校的包车,于是准备在校门口乘岀租车去科技馆,出租车收费标准如表:
(1)若出租车行驶的里程为3km,则要付车费多少元?;
(2)若出租车行驶的里程为x km(x>3),请用x的代数式表示车费y元;
(3)小胖同学身上仅有10元钱,够不够支付乘出租车到科技馆的车费?请说明理由.
| 里程(单位:km) | 收费(单位:元) |
| 3km以下(含3km) | 8.0 |
| 3km以上(每增加1km) | 1.80 |
(2)若出租车行驶的里程为x km(x>3),请用x的代数式表示车费y元;
(3)小胖同学身上仅有10元钱,够不够支付乘出租车到科技馆的车费?请说明理由.
10.下列抛物线顶点坐标为(-2,3)的是( )
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
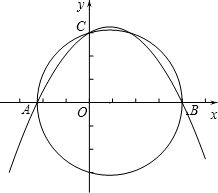 如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)
如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C) 如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.
如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.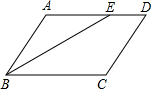 如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.
如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.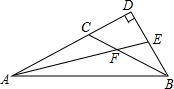 如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.
如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.