题目内容
5．先化简后再从0，1，2这三个数中选择一个适当的数代入求值：$\frac{{x}^{2}-16}{{x}^{2}-2x}$÷（x-4）-$\frac{1}{x-2}$．分析 首先把除法转化为乘法，计算乘法，在对分式通分相减，最后代入适当的x的值代入求解．
解答 解：原式=$\frac{（x+4）（x-4）}{x（x-2）}$•$\frac{1}{x-4}$-$\frac{1}{x-2}$
=$\frac{x+4}{x（x-2）}$-$\frac{1}{x-2}$
=$\frac{x+4}{x（x-2）}$-$\frac{x}{x（x-2）}$=$\frac{4}{x（x-2）}$．
当x=1时，（x≠0，2，）原式=$\frac{4}{1×（1-2）}$=-4．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
4．
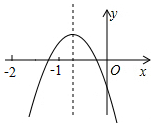二次函数y=ax2+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（ ）
二次函数y=ax2+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（ ）| A． | 4ac＜b2 | B． | abc＜0 | C． | b+c＞3a | D． | a＜b |
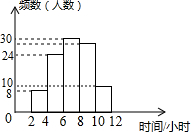为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（ ）