Question

1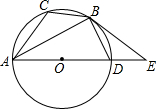．如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB．
（1）求证：BE是⊙O的切线；
（2）若BC=$\sqrt{3}$，AC=5，求圆的直径AD及切线BE的长．

Answer 1

分析 （1）先根据等弦所对的劣弧相等，再结合∠EBD=∠CAB从而得到∠BAD=∠EBD，最后用直径所对的圆周角为直角即可；
（2）利用三角形的中位线先求出OF，再用平行线分线段成比例定理求出半径R，最后根据相似求出BE即可．

解答 解：如图，

连接OB，∵BD=BC，
∴∠CAB=∠BAD，
∵∠EBD=∠CAB，
∴∠BAD=∠EBD，
∵AD是⊙O的直径，
∴∠ABD=90°，OA=BO，
∴∠BAD=∠ABO，
∴∠EBD=∠ABO，
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°，
∵点B在⊙O上，
∴BE是⊙O的切线，

（2）如图2，

设圆的半径为R，连接CD，
∵AD为⊙O的直径，
∴∠ACD=90°，
∵BC=BD，
∴OB⊥CD，
∴OB∥AC，
∵OA=OD，
∴OF=$\frac{1}{2}$AC=$\frac{5}{2}$，
∵四边形ACBD是圆内接四边形，
∴∠BDE=∠ACB，
∵∠DBE=∠ACB，
∴△DBE∽△CAB，
∴$\frac{DB}{AC}=\frac{DE}{BC}$，
∴$\frac{\sqrt{3}}{5}=\frac{DE}{\sqrt{3}}$，
∴DE=$\frac{3}{5}$，
∵∠OBE=∠OFD=90°，
∴DF∥BE，
∴$\frac{OF}{OB}=\frac{OD}{OE}$=$\frac{DF}{BE}$，
∴$\frac{\frac{5}{2}}{R}=\frac{R}{R+\frac{3}{5}}$，
∵R＞0，
∴R=3，
∴AD=2R=6，
在Rt△ODF中，OF=$\frac{5}{2}$，OD=R=3，
∴DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\frac{\sqrt{11}}{2}$
∵$\frac{OF}{OB}=\frac{DF}{BE}$，
∴BE=$\frac{OB•DF}{OF}$=$\frac{3×\frac{\sqrt{11}}{2}}{\frac{5}{2}}$=$\frac{3\sqrt{11}}{5}$

点评 此题是切线的判定，主要考查了圆周角的性质，切线的判定，平行线分线段成比例定理，相似三角形的判定和相似，圆内接四边形的性质，解本题的关键是作出辅助线．