题目内容
13. 对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y=$\sqrt{3}$x-3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为($\sqrt{3}$-$\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$)或($\sqrt{3}$$+\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y=$\sqrt{3}$x-3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为($\sqrt{3}$-$\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$)或($\sqrt{3}$$+\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
分析 根据“伴侣矩形”的定义可知:圆上的点一定在矩形的对角线交点上,因为只有对角线交点到四个顶点的距离相等,由此画出图形,先求出直线与x轴和y轴两交点的坐标,和矩形的长和宽;
有两种情况:①矩形在x轴下方时,作辅助线构建相似三角形得比例式,分别求出DG和DH的长,从而求出CG的长,根据坐标特点写出点C的坐标;②矩形在x轴上方时,也分别过C、B两点向两坐标轴作垂线,利用平行相似得比例式,求出:C($\sqrt{3}$$+\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
解答  解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,
解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,
根据直线l:y=$\sqrt{3}$x-3得:OM=$\sqrt{3}$,ON=3,
由勾股定理得:MN=$\sqrt{(\sqrt{3})^{2}+{3}^{2}}$=2$\sqrt{3}$,
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,
由cos∠ABD=cos∠ONM=$\frac{ON}{MN}$=$\frac{AB}{BD}$,
∴$\frac{3}{2\sqrt{3}}$=$\frac{AB}{2}$,AB=$\sqrt{3}$,则AD=1,
∵DG∥y轴,
∴△MDG∽△MNO,
∴$\frac{DG}{ON}=\frac{DM}{MN}$,
∴$\frac{DG}{3}=\frac{2-1}{2\sqrt{3}}$,
∴DG=$\frac{\sqrt{3}}{2}$,
∴CG=$\frac{\sqrt{3}}{2}$+$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
同理可得:$\frac{DH}{OM}=\frac{DN}{MN}$,
∴$\frac{DH}{\sqrt{3}}$=$\frac{2\sqrt{3}-1}{2\sqrt{3}}$,
∴DH=$\sqrt{3}-\frac{1}{2}$,
∴C($\sqrt{3}$-$\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$);
②矩形在x轴上方时,同理可得:C($\sqrt{3}$$+\frac{3}{2}$,$\frac{\sqrt{3}}{2}$);
故答案为:($\sqrt{3}$-$\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$)或($\sqrt{3}$$+\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
点评 此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.同时,正确理解题意准确画出符合条件的矩形是本题的关键,这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等.

| A. | -2,-2 | B. | 2,2 | C. | 0,4 | D. | -2,2 |
| A. | 0.02 | B. | 0.11 | C. | 0.1 | D. | 0.12 |
| A. | -$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
 如图,直线a、b被直线c所截,若a∥b,∠1=60°,那么∠2的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=60°,那么∠2的度数为( )| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
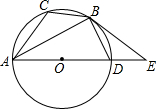 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
 如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.
如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.