题目内容
12．化简：$\frac{a-2}{a-1}$•$\frac{{a}^{2}-1}{{a}^{2}-4a+4}$．分析 先因式分解，再约分计算即可求解．
解答 解：$\frac{a-2}{a-1}$•$\frac{{a}^{2}-1}{{a}^{2}-4a+4}$
=$\frac{a-2}{a-1}$•$\frac{（a+1）（a-1）}{（a-2）^{2}}$
=$\frac{a+1}{a-2}$．
点评 考查了分式的乘除法，规律方法总结：分式乘除法的运算，归根到底是乘法的运算，当分子和分母是多项式时，一般应先进行因式分解，再约分．
练习册系列答案
相关题目
3．数据-2，-2，2，2的中位数及方差分别是（ ）
| A． | -2，-2 | B． | 2，2 | C． | 0，4 | D． | -2，2 |
20．
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{5}{4}$ | D． | $\frac{4}{5}$ |
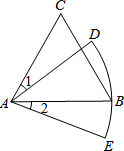如图，△ABC是等边三角形，AC=9，以点A为圆心，AB长为半径画$\widehat{DE}$，若∠1=∠2，则$\widehat{DE}$的长为3π（结果保留π）．
如图，已知在△ABC中，点D在边AC上，CD：AD=1：2，$\overrightarrow{BA}=\overrightarrow a$，$\overrightarrow{BC}=\overrightarrow b$，
4．下列各数中，最小的是（ ）
| A． | 0.02 | B． | 0.11 | C． | 0.1 | D． | 0.12 |
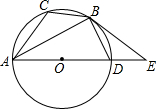如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB．
2．
如图，直线a、b被直线c所截，若a∥b，∠1=60°，那么∠2的度数为（ ）
如图，直线a、b被直线c所截，若a∥b，∠1=60°，那么∠2的度数为（ ）| A． | 120° | B． | 90° | C． | 60° | D． | 30° |