题目内容
3.解方程:(1)2x2+3=7x
(2)x2-4x-3=0.
分析 (1)移项后得到2x2-7x+3=0,然后分解因式得到(2x-1)(x-3)=0,即可得出两个一元一次方程,求出方程的解即可;
(2)利用公式法直接求出方程的解.
解答 解:(1)∵2x2+3=7x,
∴2x2-7x+3=0,
∴(2x-1)(x-3)=0,
∴2x-1=0或x-3=0,
∴x1=$\frac{1}{2}$,x2=3;
(2)∵x2-4x-3=0,
∴a=1,b=-4,c=-3,
∴△=b2-4ac=16-4×(-3)=28,
∴x=$\frac{4±\sqrt{28}}{2}$,
∴x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$.
点评 本题主要考查了解一元二次方程的知识,根据方程的特点,灵活选择解方程的方法,一般能用因式分解法的要用因式分解法,难以用因式分解法的再用公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知:4x=9y=6,则$\frac{1}{x}$+$\frac{1}{y}$等于( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
3.下面说法正确的是( )
| A. | 几个有理数相乘,当负因数有奇数个时积为负 | |
| B. | 近似数3.0万精确到千位 | |
| C. | 一个数的平方一定小于这个数 | |
| D. | 若|a|=-a,则a<0 |
18.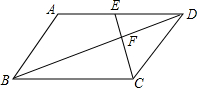 如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
 如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,测量小玻璃管口径的量具ABC,AB的长为30cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是20cm.
如图,测量小玻璃管口径的量具ABC,AB的长为30cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是20cm. 已知AB⊥BC,AD⊥DC,且BC=DC,求证:∠ABD=∠ADB.
已知AB⊥BC,AD⊥DC,且BC=DC,求证:∠ABD=∠ADB. 小亮和小颖想用下面的方法测量学校教学楼的高度:如图,小亮蹲在地上,小颖站在小亮和教学楼之间,两人适当调整自己的位置,当楼的顶部M、小颖的头部B及小亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=2m,小颖与教学楼之间的距离DN=38m,(C、D、M在同一直线上),小颖的身高BD=1.6m,小亮蹲地观测时眼睛到底面的距离AC=1m.请你根据以上测量数据帮助他们求出教学楼的高度.
小亮和小颖想用下面的方法测量学校教学楼的高度:如图,小亮蹲在地上,小颖站在小亮和教学楼之间,两人适当调整自己的位置,当楼的顶部M、小颖的头部B及小亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=2m,小颖与教学楼之间的距离DN=38m,(C、D、M在同一直线上),小颖的身高BD=1.6m,小亮蹲地观测时眼睛到底面的距离AC=1m.请你根据以上测量数据帮助他们求出教学楼的高度.