题目内容
3. 如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.
如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.(1)求双曲线的解析式;
(2)直线y=mx-4(m>0)交x轴于D点,若直线AC将△AOD的面积分为1:2的两部分,求m的值.
分析 (1)根据直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$,可以设出点C的坐标,得到∠COB的度数,从而可以求得点C的坐标,进而可以求得双曲线的解析式;
(2)根据题意可分别表示出△AOB和△ABD的面积,根据直线AC将△AOD的面积分为1:2的两部分,可知分两种情况,分别求出m的值即可.
解答 解:(1)设点C的坐标是(a,2a-4),
∵sin∠COB=$\frac{\sqrt{2}}{2}$,
∴∠COB=45°,
∴tan∠COB=$\frac{2a-4}{a}=tan45°=1$,
解得,a=4,
∴点C为(4,4),
∵点C在双曲线y=$\frac{k}{x}$(x>0)上,
∴4=$\frac{k}{4}$,得k=16,
即双曲线的解析式为:y=$\frac{16}{x}$;
(2)∵直线y=mx-4(m>0)交x轴于D点,
∴点D的坐标是($\frac{4}{m}$,0),
∵直线y=2x-4分别交坐标轴于A、B两点,
∴点A的坐标是(0,-4),B(2,0),
∵直线AC将△AOD的面积分为1:2的两部分,
∴$\frac{OB•OA}{2}:\frac{BD•OA}{2}=\frac{1}{2}$或$\frac{OB•OA}{2}:\frac{BD•OA}{2}=\frac{2}{1}$,
即$\frac{2×4}{2}:\frac{(\frac{4}{m}-2)•4}{2}=\frac{1}{2}$或$\frac{2×4}{2}:\frac{(\frac{4}{m}-2)•4}{2}=\frac{2}{1}$,
解得,m=$\frac{2}{3}$或m=$\frac{4}{3}$,
即m的值是$\frac{2}{3}$或$\frac{4}{3}$.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合和分类讨论的数学思想解答问题.

 名校课堂系列答案
名校课堂系列答案| 分数段 | 90<x≤100 | 80<x≤90 | 70<x≤80 | 60<x≤70 | 0≤x≤60 |
| 人数 | 100 | 200 | 80 | 80 | 40 |
②若用扇形统计图表示统计结果,则分数段为90<x≤100的人数所对应扇形的圆心角的度数为72°;
(2)试估算抽取学生地理会考模拟测试的平均成绩.
| 汽车行驶速度v(千米/小时) | 30 | 40 | 50 | 60 | 70 |
| 制动距离s(米) | 5 | 12 | 19 | 26 | 33 |
(2)若s是v的一次函数,求s关于v的函数解析式.
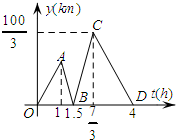 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题: 如图,AD⊥BD,AC⊥BC,AD与BC交于点O,AD=BC.
如图,AD⊥BD,AC⊥BC,AD与BC交于点O,AD=BC. 如图,AD∥BC,AC2=AD•BC,求证;∠B=∠DCA.
如图,AD∥BC,AC2=AD•BC,求证;∠B=∠DCA.