题目内容
1.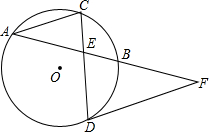 如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.
如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.(1)求证:DF=EF;
(2)连接AC,若AC∥DF,⊙O的半径为$\frac{25}{3}$,BE=$\frac{3}{5}$AE,求CE的长.
分析 (1)连接OC,OD,根据垂径定理得到OC⊥AB,求得∠OCE+∠CEA=∠OCE+∠FED=90°,由DF是⊙O的切线,得到OD⊥DF,得到∠ODC+∠EDF=90°,等量代换得到∠DEF=∠EDF,于是得到结论;
(2)如图,作辅助线;证明OH⊥AB,AH=4λ,此为解题的关键性结论;证明CE=$\sqrt{10}$;列出方程r2=(r-3λ)2+(4λ)2,求出λ=$\frac{6}{25}$r=2,即可解决问题.
解答 解:(1)连接OC,OD,
∵C为$\widehat{AB}$的中点,
∴OC⊥AB,
∴∠OCE+∠CEA=∠OCE+∠FED=90°,
∵DF是⊙O的切线,
∴OD⊥DF,
∴∠ODC+∠EDF=90°,
∵OC=OD,
∴∠OCD=∠ODC,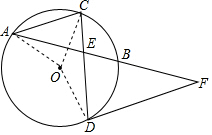
∴∠DEF=∠EDF,
∴EF=DF;
(2)如图,连接OA、OC;
由(1)知OC⊥AB,
∴AH=BH;
∵AC∥DF,
∴∠ACD=∠CDF;而EF=DF,
∴∠DEF=∠CDF=∠ACD,
∴AC=AE;
设AE=5λ,则BE=3λ,
∴AH=4λ,HE=λ,AC=AE=5λ;
∴由勾股定理得:CH=3λ;
CE2=CH2+HE2=9λ2+λ2,
∴CE=$\sqrt{10}$;
在直角△AOH中,由勾股定理得:
AO2=AH2+OH2,
即r2=(r-3λ)2+(4λ)2,
解得:λ=$\frac{6}{25}$r=$\frac{6}{25}$×$\frac{25}{3}$=2,
∴CE=2$\sqrt{10}$.
点评 该题主要考查了圆的切线的性质的应用问题,垂径定理,勾股定理,解题的关键是作辅助线;灵活运用有关定理来分析、解答.

练习册系列答案
相关题目
12.在一个不透明的口袋里,装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)请估计当n很大时,摸到白球的频率将会接近?
(2)假如你去摸一次,你摸到白球的概率是多少?试估算口袋中黑、白两种颜色的球各有多少个?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(2)请估计当n很大时,摸到白球的频率将会接近?
(2)假如你去摸一次,你摸到白球的概率是多少?试估算口袋中黑、白两种颜色的球各有多少个?
 如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.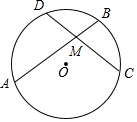 如图,已知圆O,弦AB、CD相交于点M,M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.
如图,已知圆O,弦AB、CD相交于点M,M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.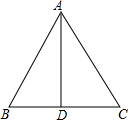 在△ABC中,AB=AC,AD是BC边上的中线,若△ABC的周长为36,△ABD的周长为30,求AD的长.
在△ABC中,AB=AC,AD是BC边上的中线,若△ABC的周长为36,△ABD的周长为30,求AD的长.