题目内容
在Rt△ABC中，∠C=90°，sinB=
，则tanA的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
考点：互余两角三角函数的关系
专题：
分析：利用sinB=
，分别表示出AB，BC，AC的长，再利用锐角三角函数关系得出tanA的值．
| 1 |
| 3 |
解答：
解：∵∠C=90°，sinB=
，
∴设AC=x，AB=3x，则BC=2
x，
则tanA=
=
=2
．
故选：C．
解：∵∠C=90°，sinB=| 1 |
| 3 |
∴设AC=x，AB=3x，则BC=2
| 2 |
则tanA=
| BC |
| AC |
2
| ||
| x |
| 2 |
故选：C．
点评：此题主要考查了锐角三角函数关系，表示出三角形各边长是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
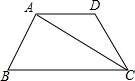在梯形ABCD中，AD∥BC，AB=AD=DC，∠B=∠BCD=60°，连接AC．求cos∠ACB的值．
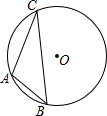如图，⊙O为△ABC的外接圆，
如图所示，在矩形ABCD中，DE⊥AC于点E，设∠ADE=a，且cosa=| 3 |
| 5 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
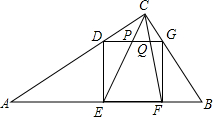如图，△ABC中，∠C=90°，AC=4，BC=3，正方形DEFG的四个顶点分别在边AC、AB、CB上．
如图，已知点O在直线CD上，当∠1和∠2满足条件