题目内容
写出一个图象经过一，三象限的一次函数y=kx+b（k≠0）的解析式（关系式） ．
考点：一次函数的性质
专题：开放型
分析：根据k、b的符号来求确定一次函数y=kx+b的图象所经过的象限．
解答：解：∵一次函数的图象经过第一、三象限，
∴一次函数y=kx+b（k≠0）中的k＞0，
如：y=2x+2（答案不唯一）．
故答案是：y=2x+2．
∴一次函数y=kx+b（k≠0）中的k＞0，
如：y=2x+2（答案不唯一）．
故答案是：y=2x+2．
点评：本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
练习册系列答案
全能练考卷系列答案
相关题目
在Rt△ABC中，∠C=90°，sinB=
，则tanA的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
在-（-2），|-3|，0，（-1）2，（-2）3这五个数中，正数的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，在Rt△ABC中，∠C=90°，AD是△CAB的平分线，DE垂直平分AB，若CD=3，则BD=
如图所示，如果?ABCD的一内角∠BAD的平分线交BC于点E，且AE=BE，求?ABCD各内角的度数．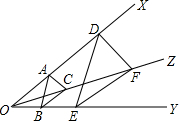
如图，点A，D在∠XOY的边OX上，点B，E在OY边上，射线OZ在∠XOY内，且点C，F在OZ上，AC∥DF，BC∥EF．
如图，已知DE∥AB，FE∥DB，BD平分∠ABC．求证：EF平分∠CED．