题目内容
8．
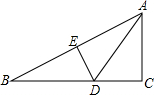如图，△ABC中，∠ACB=90°，∠B=30°，DE垂直平分AB，若DE=1.5cm，则BC的长是（ ）| A． | 3cm | B． | 4.5cm | C． | 6cm | D． | 7.5cm |
分析 根据线段垂直平分线求出AD=BD，根据含30°角的直角三角形性质求出AD=BD=2DE=3cm，根据含30°角的直角三角形性质求出DC，即可得出答案．
解答 解：∵DE垂直平分AB，
∴AD=BD，∠DEB=90°，
∴∠DAE=∠B=30°，
∵∠B=30°，DE=1.5cm，
∴AD=BD=2DE=3cm，
∵∠C=90°，∠B=30°，
∴∠CAB=60°，
∴∠CAD=60°-30°=30°，
∴DC=$\frac{1}{2}$AD=1.5cm，
∴BC=BD+DC=3cm+1.5cm=4.5cm，
故选B．
点评 本题考查了线段垂直平分线性质，含30°角的直角三角形性质的应用，能运用性质定理求出AD=BD，BD=2DE和DC=$\frac{1}{2}$AD是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
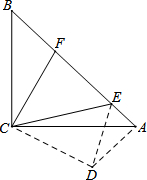已知，如图，在Rt△ABC中，∠ACB=90°，AC=BC，点E、F分别是斜边AB上的两点，且∠FCE=45°．
如图，抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B，A（0，3），C（6，0），则图中抛物线与矩形OABC形成的阴影部分的面积的和为（ ）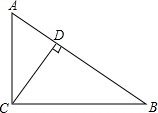
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，tan∠ACD=$\frac{3}{4}$，AB=5，那么CD的长是$\frac{12}{5}$．
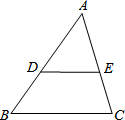如图，在△ABC中，DE∥BC，AD=3cm，BD=2cm，则△ADE与△ABC的相似比为$\frac{3}{5}$．
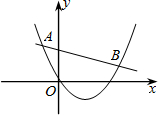如图所示，已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（-2，4），B（8，2）．根据图象回答：