题目内容
12. 如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据角平分线的做法可得①正确,再根据直角三角形的高的定义可得②正确,然后计算出∠CAD=∠DAB=29°,可得AD≠BD,根据到线段两端点距离相等的点在线段的垂直平分线上,因此③错误,根据三角形内角和可得④正确.
解答 解:根据作法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,
∴CD是△ADC的高,故②正确;
∵∠C=90°,∠B=32°,
∴∠CAB=58°,
∵AD是∠BAC的平分线,
∴∠CAD=∠DAB=29°,
∴AD≠BD,
∴点D不在AB的垂直平分线上,故③错误;
∵∠CAD=29°,∠C=90°,
∴∠CDA=61°,故④正确;
共有3个正确,
故选:C.
点评 此题主要考查了基本作图,关键是掌握角平分线的做法和线段垂直平分线的判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列水平放置的几何体中,俯视图是矩形的是( )
| A. | 圆柱 | B. | 长方体 | C. | 三棱柱 | D. | 圆锥 |
3.下列等式成立的是( )
| A. | 2-2=-22 | B. | 26÷23=22 | C. | (23)2=25 | D. | 20=1 |
7.下列图形既可看成轴对称图形又可看成中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.甲、乙两班参加市统考,两班的平均分和方差分别为$\overline{{X}_{甲}}$=86分,$\overline{{X}_{乙}}$=86分,S甲2=263,S乙2=236,那么成绩较为整齐的是( )
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
1.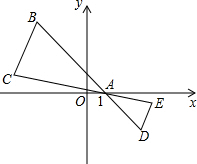 如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )
如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )
 如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )
如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )| A. | $\frac{1}{2}$(a-1) | B. | $\frac{1}{2}$(a+1) | C. | 3-2a | D. | 2(a-1) |
 如图,A,B,C是⊙O上三点,已知∠ACB=α,则∠AOB=360°-2α.(用含α的式子表示)
如图,A,B,C是⊙O上三点,已知∠ACB=α,则∠AOB=360°-2α.(用含α的式子表示)