题目内容
 在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,求点D到AB的距离.
在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,求点D到AB的距离.考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线,证明AE=DE;证明△BDE∽△BCA,得到
=
,列出比例式即可解决问题.
| BE |
| AB |
| DE |
| AC |
解答: 解:如图,过点D作DE⊥AB于点E.
解:如图,过点D作DE⊥AB于点E.
则DE∥AC;
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,∠ADE=90°-45°=45°,
∴AE=DE(设为λ),
则BE=3-λ;
∵DE∥AC,
∴△BDE∽△BCA,
∴
=
,即:
=
,
解得:λ=
,
∴点D到AB的距离=
.
 解:如图,过点D作DE⊥AB于点E.
解:如图,过点D作DE⊥AB于点E.则DE∥AC;
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,∠ADE=90°-45°=45°,
∴AE=DE(设为λ),
则BE=3-λ;
∵DE∥AC,
∴△BDE∽△BCA,
∴
| BE |
| AB |
| DE |
| AC |
| 3-λ |
| 3 |
| λ |
| 4 |
解得:λ=
| 12 |
| 7 |
∴点D到AB的距离=
| 12 |
| 7 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造相似三角形;灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
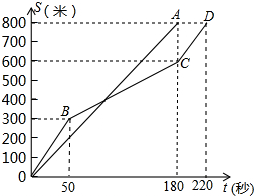 在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )
在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )| A、甲比乙先到达终点 |
| B、跑步过程中甲的速度不变 |
| C、起跑后400米内,乙始终在甲的前面 |
| D、在起跑后180米时,甲乙两人相遇 |
在数轴上表示不等式组
的解,其中正确的是( )
|
A、 |
B、 |
C、 |
D、 |
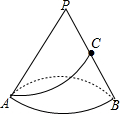 有一个圆锥体形状的粮仓,如图所示,一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食,已知圆锥底面积为25πcm2,母线长为10cm,若猫在粮仓面上捉老鼠,则猫出A点到C点的最短路程是多少?
有一个圆锥体形状的粮仓,如图所示,一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食,已知圆锥底面积为25πcm2,母线长为10cm,若猫在粮仓面上捉老鼠,则猫出A点到C点的最短路程是多少?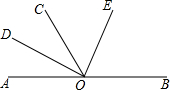 如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,
如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,