题目内容
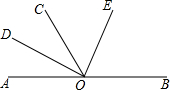 如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,
如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,(1)求出∠BOD的度数;
(2)说明OE是∠BOC的平分线.
考点:余角和补角,角平分线的定义
专题:
分析:(1)根据∠AOC=60°,OD平分∠AOC求出∠AOD的度数,根据补角的定义即可得出∠BOD的度数;
(2)根据∠AOC=60°求出∠BOC的度数,再由OD平分∠AOC求出∠DOC的度数,根据∠DOC与∠COE互余即可得出∠COE的度数,进而可得出结论.
(2)根据∠AOC=60°求出∠BOC的度数,再由OD平分∠AOC求出∠DOC的度数,根据∠DOC与∠COE互余即可得出∠COE的度数,进而可得出结论.
解答:解:(1)∵∠AOC=60°,OD平分∠AOC,
∴∠AOD=30°,
∴∠BOD=180°-30°=150°;
(2)∵∠AOC=60°,
∴∠BOC=120°.
∵OD平分∠AOC,
∴∠DOC=
×60°=30°.
∵∠DOC与∠COE互余,
∴∠COE=90°-30°=60°,
∴∠COE=
∠BOC,即OE是∠BOC的平分线.

∴∠AOD=30°,
∴∠BOD=180°-30°=150°;
(2)∵∠AOC=60°,
∴∠BOC=120°.
∵OD平分∠AOC,
∴∠DOC=
| 1 |
| 2 |
∵∠DOC与∠COE互余,
∴∠COE=90°-30°=60°,
∴∠COE=
| 1 |
| 2 |
点评:本题考查的是余角和补角,熟知余角和补角的定义是解答此题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米. 在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,求点D到AB的距离.
在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,求点D到AB的距离. 如图,△ABC的两条中线BE、CD交于点O,连接AO.
如图,△ABC的两条中线BE、CD交于点O,连接AO. 如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系:
如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系: 如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD=
如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD= 过图中点P分别画AB、BC、AC的垂线,垂足分别为D、E、F,量出点P到AB、BC、AC的距离.
过图中点P分别画AB、BC、AC的垂线,垂足分别为D、E、F,量出点P到AB、BC、AC的距离.