Question

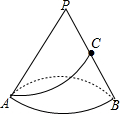有一个圆锥体形状的粮仓，如图所示，一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食，已知圆锥底面积为25πcm²，母线长为10cm，若猫在粮仓面上捉老鼠，则猫出A点到C点的最短路程是多少？

Answer 1

考点：平面展开-最短路径问题,圆锥的计算

专题：

分析：最短距离的问题首先应转化为圆锥的侧面展开图的问题，转化为平面上两点间的距离的问题．需先算出圆锥侧面展开图的扇形半径．看如何构成一个直角三角形，然后根据勾股定理进行计算．

解答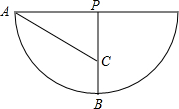：解：如图所示，
设圆锥的底面半径为r，底面弧长所对的圆周角为n，
则πr²=25π，解得r=5，
∵母线长为10cm，
∴2π×5=

nπ×10

180

，
解得n=180°，
∴∠APC=90°．
∵点C是PB的中点，
∴PC=

1

2

PB=5cm，
∴AC=

AP2+PC2

=

102+52

=5

5

（cm）．
答：猫出A点到C点的最短路程是5

5

cm．

点评：本题考查的是平面展开-最短路径问题，此类问题应先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．