题目内容
20.先化简,再求值:(1)$3{x^2}+(-\frac{3}{2}x+\frac{1}{3}{y^2})(2x-\frac{2}{3}y)$,其中$x=-\frac{1}{3}$,$y=\frac{2}{3}$.
(2)(a+b)(a-b)+(4ab3-8a2b2)÷4ab,其中a=2,b=1.
分析 (1)原式利用多项式乘以多项式法则计算,合并得到最简结果,把x与y的值代入计算即可求出值;
(2)原式第一项利用平方差公式化简,第二项利用多项式除以单项式法则计算,合并得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)原式=3x2-3x2+xy+$\frac{2}{3}$xy2-$\frac{2}{9}$y3=xy+$\frac{2}{3}$xy2-$\frac{2}{9}$y3,
当x=-$\frac{1}{3}$,y=$\frac{2}{3}$时,原式=-$\frac{2}{9}$-$\frac{8}{81}$-$\frac{16}{243}$=-$\frac{94}{243}$;
(2)原式=a2-b2+b2-2ab=a2-2ab,
当a=2,b=1时,原式=4-4=0.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列各式是最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
11.下列二次根式中,最简二次根式是( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{48}$ | C. | $\sqrt{4.8}$ | D. | $\sqrt{{x^2}+1}$ |
5.在平面直角坐标系内,点P(m-3,m-5)在第三象限,则m的取值范围是( )
| A. | -5<m<3 | B. | -3<m<5 | C. | m<3 | D. | m<5 |
 如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是OQ的长.
如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是OQ的长.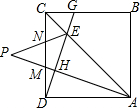 如图,在正方形ABCD中,点M、N是CD边上的两点,且DM=CN,过D作DG⊥AM于H,且分别交AC、BC于点E、G,AM、EN的延长线交于点P.
如图,在正方形ABCD中,点M、N是CD边上的两点,且DM=CN,过D作DG⊥AM于H,且分别交AC、BC于点E、G,AM、EN的延长线交于点P.