Question

5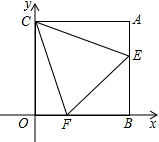．如图，在平面直角坐标系中，点A（n，m）在第一象限，AB⊥x轴于B，AC⊥y轴于C，（m-3）²+n²-6n+9=0，过C点作∠ECF分别交线段AB、OB于E、F两点．
（1）求m、n的值并写出A、B、C三点的坐标；
（2）若OF+BE=AB，求证：CF=CE．

Answer 1

分析 （1）已知等式变形后，利用非负数的性质求出m与n的值，即可确定出A，B，C的坐标；
（2）由AE+EB=AB，以及OF+BE=AB，得到AE=OF，根据四边形ABOC为正方形，得到CA=CO，且∠A=∠COF=90°，利用SAS得到三角形ACE与三角形OCF全等，利用全等三角形对应边相等得到CF=CE；

解答 解：（1）将（m-3）²+n²=6n-9变形得：（m-3）²+（n-3）²=0，
∴m=3，n=3，
∴A（3，3），B（3，0），C（0，3）；
（2）∵OF+BE=AB，AE+EB=AB，
∴AE=OF，
∵四边形ABCD为正方形，
∴AC=OC，∠A=∠COF=90°，
在△ACE和△OCF中，
$\left\{\begin{array}{l}{AC=OC}\\{∠A=∠COF}\\{AE=OF}\end{array}\right.$，
∴△ACE≌△OCF（SAS），
∴CF=CE；

点评 此题涉及的知识有：坐标与图形性质，全等三角形的判定与性质，非负数的性质，正方形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．