题目内容
17. 如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.(1)求证:AD=EC;
(2)若BC=2AD,AB=AO=m,求证:S四边形ADCE=m2.(其中S表示四边形ADCE的面积)
分析 (1)由AE∥BC,DE∥AB,可证得四边形ABDE为平行四边形,又由AD是边BC上的中线,可得AE=CD,即可证得四边形ADCE 是平行四边形,继而证得结论;
(2)由BC=2AD,易得四边形ADCE 是菱形,继而求得S四边形ADCE=m2.
解答 证明:(1)∵AE∥BC,DE∥AB,
∴四边形ABDE为平行四边形,
∴AE=BD,
∵BD=CD,
∴AE=CD,
∴四边形ADCE 是平行四边形,
∴AD=CE;
(2)∵BC=2AD,BC=2CD,
∴AD=CD,
∵四边形ADCE 是平行四边形,
∴四边形ADCE 是菱形,
∵DE=AB=m,AC=2AO=2m,
∴S四边形ADCE=$\frac{1}{2}$AC•DE=m2.
点评 此题考查了平行四边形的判定与性质以及菱形的判定与性质.注意证得四边形ADCE 是平行四边形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示的是由5个边长是1的正方形组成的图形.
如图所示的是由5个边长是1的正方形组成的图形. 正方形ABCD中,E、F分别为中点,求EG:GH:HC.
正方形ABCD中,E、F分别为中点,求EG:GH:HC.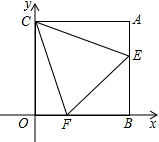 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. 如图,已知∠A=∠B,OA=OB,AD与BC相交于点E,则OE平分∠AOB吗?说明理由.
如图,已知∠A=∠B,OA=OB,AD与BC相交于点E,则OE平分∠AOB吗?说明理由. 如图,△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,B,C,D在同一直线上,连接EC.求证:EC⊥BD.
如图,△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,B,C,D在同一直线上,连接EC.求证:EC⊥BD. 小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题: 如图,线段AB,CD相交于点O,AD∥CB,AO=2,AB=5,求$\frac{DO}{OC}$.
如图,线段AB,CD相交于点O,AD∥CB,AO=2,AB=5,求$\frac{DO}{OC}$.