题目内容
16.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.(1)求证:OE=OF;
(2)如图(2)若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

分析 (1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.
(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
解答 解:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵$\left\{\begin{array}{l}{∠BOE=∠AOF}\\{BO=AO}\\{∠BEO=∠AFO}\end{array}\right.$,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵$\left\{\begin{array}{l}{∠BOE=∠AOF}\\{BO=AO}\\{∠F=∠E}\end{array}\right.$,
∴△BOE≌△AOF.
∴OE=OF.
点评 本题主要考查正方形的性质和全等三角形的判定与性质,将待求线段放到两个三角形中,通过证明三角形全等得到对应边相等是解题的关键.

练习册系列答案
相关题目
4.关于坐标系,下列说法正确的是( )
| A. | 建立坐标系,是为了定量地描述物体的位置及位置的变化 | |
| B. | 在建立坐标系时只需要确定正方向即可,与规定的正方向同向为正,与规定的正方向反向则为负 | |
| C. | 只能在水平方向建立直线坐标系 | |
| D. | 建立好直线坐标系后,可以用(x,y)表示物体的位置 |
 如图所示的是由5个边长是1的正方形组成的图形.
如图所示的是由5个边长是1的正方形组成的图形. 在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论:
在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论: 正方形ABCD中,E、F分别为中点,求EG:GH:HC.
正方形ABCD中,E、F分别为中点,求EG:GH:HC.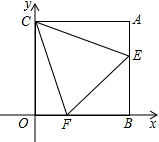 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. 小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题: