题目内容
13. 在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD.
在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD.
分析 根据题目中的条件可以得到AD和CD的关系,∠EAD的度数,从而可以证明结论.
解答 证明:∵在△ABC中,∠BAC=90°,AB=AC,D为BC中点,
∴AD=$\frac{1}{2}BC$=BD=CD,∠EAD=∠FCD=45°,
在△AED和△CFD中,
$\left\{\begin{array}{l}{EA=FC}\\{∠EAD=∠FCD}\\{AD=CD}\end{array}\right.$,
∴△AED≌△CFD(SAS).
点评 本题考查全等三角形的判定,解题的关键是明确题意,找出所证结论需要的条件.

练习册系列答案
相关题目
4.关于坐标系,下列说法正确的是( )
| A. | 建立坐标系,是为了定量地描述物体的位置及位置的变化 | |
| B. | 在建立坐标系时只需要确定正方向即可,与规定的正方向同向为正,与规定的正方向反向则为负 | |
| C. | 只能在水平方向建立直线坐标系 | |
| D. | 建立好直线坐标系后,可以用(x,y)表示物体的位置 |
18.学校开展“献爱心”捐款活动,某班50名同学积极参加了这次活动,下表是李华同学对全班捐款情况的统计表:
已知全班平均每人捐款11.4元.请求出A、B的值.
| 捐 款 (元) | 5 | 10 | 20 | A | 30 |
| 人 数 | 18 | 20 | B | 4 | 2 |
 正方形ABCD中,E、F分别为中点,求EG:GH:HC.
正方形ABCD中,E、F分别为中点,求EG:GH:HC.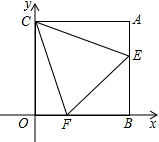 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.