题目内容
18.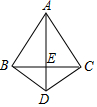 如图,在△ABC中,AB=AC,∠ABC=60°,D是三角形外一点,且BD=CD,AD与BC交于一点E,∠BDC=120°,则下列结论错误的是( )
如图,在△ABC中,AB=AC,∠ABC=60°,D是三角形外一点,且BD=CD,AD与BC交于一点E,∠BDC=120°,则下列结论错误的是( )| A. | AD垂直平分BC | B. | AB=2BD | C. | ∠ACD=90° | D. | △ABD≌△ACD |
分析 根据线段垂直平分线的性质、全等三角形的判定定理判断即可.
解答 解:∵AB=AC,BD=CD,
∴直线AD是线段BC的垂直平分线,
∴AD垂直平分BC,∴A符合题意;
∵∠ABC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,又∠BDC=120°,
∴∠ABC=∠ACD=90°,∴C符合题意;
∵∠ABC=60°,
∴∠BAD=30°,
∴AD=2BD,∴B不符合题意;
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD,∴D符合题意,
故选:B.
点评 本题考查的是线段垂直平分线的性质、全等三角形的判定,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
8.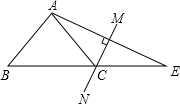 如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
 如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 48° | C. | 50° | D. | 72° |
9.某汽车厂原计划上半年每月生产汽车20辆,实际生产量规定超过20辆记为“+”,不足20辆记为“-”,实际每月生产量与计划每月生产量相比情况如下表:
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
(2)上半年内的实际总生产量是怎么变化的?
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 增减量/辆 | +3 | -2 | -1 | +4 | +2 | -5 |
(2)上半年内的实际总生产量是怎么变化的?
7. 已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
 已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )
已知:AB∥CD,∠1=80°,∠2=50°,则∠ADC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
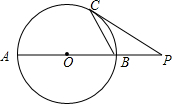 如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小.
如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小. 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.