题目内容
13.已知二次函数C1:y=ax2+4ax(a≠0)的图象顶点为M,显然它与x轴一定有两个不同的交点.(1)求二次函数C1与x轴的两个交点的坐标;
(2)若二次函数C1与一次函数y=-x-4只有一个交点,求二次函数C1的解析式;
(3)将二次函数C1绕原点中心对称得到求二次函数C2,
①直接写出求二次函数C2的解析式(用含a式子表示);
②二次函数C2的图象能否经过二次函数C1的图象顶点M?说明理由;
③直线x=1与二次函数C1、C2分别交于P、Q两点,已知:PQ=2,求二次函数C1的解析式.
分析 (1)将y=0代入二次函数C1:y=ax2+4ax(a≠0)中,即可求得二次函数C1与x轴的两个交点的坐标;
(2)令ax2+4ax=-x-4,化为二元一次方程的一般形式,然后令△=0,即可求得a的值,从而可以求得二次函数C1的解析式;
(3)①根据二次函数C1绕原点中心对称得到求二次函数C2,从而可以求得二次函数C2的解析式;
②根据一次函数C1的解析式可以求得它的顶点坐标,然后代入二次函数C2的解析式中,即可解答本题;
③根据题意可以分别求得P、Q的坐标,从而可以求得a的值,进而得到二次函数C1的解析式.
解答 解:(1)∵y=ax2+4ax=ax(x+4),
∴y=0时,ax(x+4)=0,
解得,x1=0,x2=-4,
即二次函数C1与x轴的两个交点的坐标(0,0),(-4,0);
(2)∵二次函数C1与一次函数y=-x-4只有一个交点,
∴ax2+4ax=-x-4
∴ax2+(4a+1)x+4=0,
∴△=(4a+1)2-4a×4=0,
解得,a=$\frac{1}{4}$,
∴二次函数C1的解析式是y=$\frac{1}{4}{x}^{2}+x$;
(3)①二次函数C1绕原点中心对称得到求二次函数C2,二次函数C1:y=ax2+4ax(a≠0),
∴二次函数C2的解析式是:-y=a(-x)2+4a×(-x),
化简,得y=-ax2+4ax,
即二次函数C2的解析式是y=-ax2+4ax;
②二次函数C2的图象不经过二次函数C1的图象顶点M,
∵二次函数C1:y=ax2+4ax=a(x+2)2-4a,
∴二次函数C1的顶点坐标是(-2,-4a),
将x=-2代入二次函数C2的解析式y=-ax2+4ax,得
y=-a×(-2)2+4a×(-2)=-12a,
∵-4a≠-12a,
∴二次函数C2的图象不经过二次函数C1的图象顶点M;
③当x=1时,y=ax2+4ax=a×12+4a×1=a+4a=5a,
当x=1时,y=-ax2+4ax=-a×12+4a×1=3a,
∴点P的坐标为(1,5a),点Q的坐标(1,3a),
∴PQ=|5a-3a|=|2a|,
∵PQ=2,
∴|2a|=2,
解得,a=±1,
∴二次函数C1的解析式是y=x2+4x或y=-x2-4x.
点评 本题考查抛物线与x轴的交点、一次函数图象上点的坐标特征、待定系数法求二次函数解析式,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用二次函数的性质解答.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案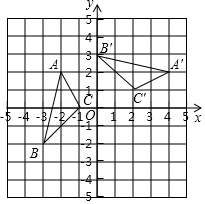 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | (0,1) | B. | (0,-1) | C. | C(1,-1) | D. | (1,0) |
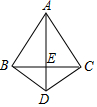 如图,在△ABC中,AB=AC,∠ABC=60°,D是三角形外一点,且BD=CD,AD与BC交于一点E,∠BDC=120°,则下列结论错误的是( )
如图,在△ABC中,AB=AC,∠ABC=60°,D是三角形外一点,且BD=CD,AD与BC交于一点E,∠BDC=120°,则下列结论错误的是( )| A. | AD垂直平分BC | B. | AB=2BD | C. | ∠ACD=90° | D. | △ABD≌△ACD |

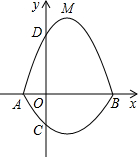 如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点. 如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).
如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).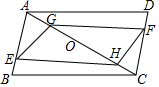 如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形.
如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形.