题目内容

8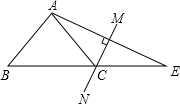．如图，在△ABE中，∠A=108°，AE的垂直平分线MN交BE于点C，且AB=CE，则∠B的度数是（　　）
A．45°B．48°C．50°D．72°

分析 根据线段的垂直平分线的性质得到CA=CE，根据等腰三角形的性质得到∠CAE=∠E，根据三角形的外角的性质得到∠ACB=2∠E，根据三角形内角和定理计算即可．

解答 解：∵MN是AE的垂直平分线，
∴CA=CE，
∴∠CAE=∠E，
∴∠ACB=2∠E，
∵AB=CE，
∴AB=AC，
∴∠B=∠ACB=2∠E，
∵∠BAE=108°，
∴∠B+∠E=72°，
∴∠B=48°，
故选B．

点评 本题考查的是线段的垂直平分线的性质，等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

练习册系列答案
相关题目
18．如图，将字母“V”向右平移2格会得到字母“W”．
19．两张宽度均为4的矩形纸片按如图所示方式放置
（1）如图①，求证：四边形ABCD是菱形．
（2）如图②，点P在BC上，PF⊥AD于F，若S四边形ABCD=16$\sqrt{2}$，PB=2，i．求∠BAD的度数；ii．求DF的长．
16．【定义】已知P为△ABC所在平面内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，若存在一个三角形与△ABC相似（全等除外），那么就称P为△ABC的“共相似点”，根据“共相似点”是否落在三角形的内部，边上或外部，可将其分为“内共相似点”，“边共相似点”或“外共相似点”．
（1）据定义可知，等边三角形不存在（填“存在”或“不存在”）共相似点．
【探究1】用边共相似点探究三角形的形状
（2）如图1，若△ABC的一个边共相似点P与其对角顶点B的连线，将△ABC分割成的两个三角形恰与原三角形均相似，试判断△ABC的形状，并说明理由．
【探究2】用内共相似点探究三角形的内角关系
（3）如图2，在△ABC中，∠A＜∠B＜∠C，高线CD与角平分线BE交于点P，若P是△ABC的一个内共相似点，试说明点E是△ABC的边共相似点，并直接写出∠A的度数．
【探究3】探究直角三角形共相似点的个数
（4）如图3，在Rt△ABC中，∠C=90°，∠A=30°，BC=$\sqrt{3}$，若△PBC与△ABC相似，则满足条件的P点共有8个，顺次连接所有满足条件的P点而围成的多边形的周长为6+$\sqrt{3}$．
3．数轴上点A对应的数为a，点B对应的数为b，且多项式x3y-2xy+5的二次项系数为a，常数项为b．
（1）直接写出：a=-2，b=5．
（2）数轴上点A、B之间有一点动P，若点P对应的数为x，试化简|2x+4|+2|x-5|-|6-x|；
（3）若点M从点A出发，以每秒1个单位长度的速度沿数轴向右移动：同时点N从点B出发，沿数轴以每秒2个单位长度的速度向左移动，到达A点后立即返回并向右继续移动，请直接写出经过2或$\frac{8}{3}$或6或8秒后，M、N两点相距1个单位长度，并选择一种情况计算说明．
13．下列汽车标志中，既是轴对称图形又是中心对称图形的是（　　）
A．B．C．D．
20．为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加，某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=-2x+80．设这种产品每天的销售利润为w元．
（1）求w与x之间的函数关系式．并指出该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
（2）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？
17．解方程：27（x+1）3+64=0．
18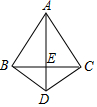．如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（　　）
A．AD垂直平分BCB．AB=2BDC．∠ACD=90°D．△ABD≌△ACD

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网