Question

2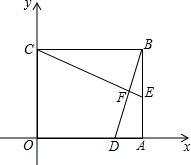．将一个矩形纸片如图所示放置在平面直角坐标系中，已知OB=5，OC=3，
（1）将纸片沿着CE对折，点B落在x轴上的点D处，求直线CD的解析式；
（2）若CE和BD交于点F，求点F的坐标．

Answer 1

分析 （1）由对折可知BC=CD=5，运用勾股定理即可求得D点的坐标，然后利用待定系数法即可得到结论；
（2）过F作FM⊥OA于M，由折叠的性质得到CE垂直平分BD，根据三角形的中位线的性质即可得到结论．

解答 解：（1）连接CD，OB，
∵四边形ABCO是矩形，
∴BC=OA，AB=OC，由折叠的性质得CD=BC=4，∴OD=$\sqrt{C{D}^{2}-O{C}^{2}}$=$\sqrt{7}$，
∴点D的坐标为（$\sqrt{7}$，0），
设直线CD的解析式为：y=kx+b，
则$\left\{\begin{array}{l}{0=\sqrt{7}k+b}\\{3=b}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=-\frac{3\sqrt{7}}{7}}\\{b=3}\end{array}\right.$
∴直线CD的解析式为：y=-$\frac{3\sqrt{7}}{7}$x+3；

（2）过F作FM⊥OA于M，
∵将纸片沿着CE对折，点B落在x轴上的点D处，
∴CE垂直平分BD，
∵FM∥AB，
∴FM=$\frac{1}{2}$AB=$\frac{3}{2}$，DM=$\frac{1}{2}$AD=$\frac{4-\sqrt{7}}{2}$，
∴OM=$\sqrt{7}$+$\frac{4-\sqrt{7}}{2}$=2+$\frac{\sqrt{7}}{2}$，
∴F（2+$\frac{\sqrt{7}}{2}$，$\frac{3}{2}$）．

点评 此题考查了折叠的性质，勾股定理，图形的对称性，待定系数法求函数解析式以及三角形的中位线，熟练掌握折叠的性质是解题的关键．