题目内容

14．已知a、b、c满足：
（1）5（a+3）2+2|b-2|=0；
（2）$\frac{1}{3}$x2-ay1+b+c+22a4b+c+1是七次单项式；
求多项式a2b-[a2b-（2abc-a2c-3a2b）-4a2c]-abc的值．．

分析 利用非负数的性质及单项式次数定义求出a，b，c的值，原式去括号合并后代入计算即可求出值．

解答 解：∵5（a+3）2+2|b-2|=0；$\frac{1}{3}$x2-ay1+b+c+22a4b+c+1是七次单项式；
∴a+3=0，b-2=0，2-a+1+b+c=7，
解得：a=-3，b=2，c=-1，
则原式=a2b-a2b+2abc-a2c-3a2b+4a2c-abc=-3a2b+3a2c+abc=-54-27+6=-75．

点评 此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
4．如图所示，在△ABC中，AB=AC，P是BC边上的一点，PE⊥AB，PF⊥AC，BD是AC边上的高，试探究PE+PF与BD之间的数量关系．
5．⊙O的半径为6cm，当圆心O到直线l的距离d=6cm时，直线l与圆有1个交点；当d＜6cm时，直线l与圆有2个交点．
2．解方程：
（1）x2+3x-2=0；
（2）（x+1）（x-1）=2$\sqrt{2}x$；
（3）$\frac{x+2}{3}$-$\frac{{x}^{2}-3}{2}$=2．
9．已知y1=$\sqrt{2}$x，y2=$\frac{2}{{y}_{1}}$，y3=$\frac{2}{{y}_{2}}$，y4=$\frac{2}{{y}_{3}}$，…，y2014=$\frac{2}{{y}_{2013}}$，则y1•y2014等于（　　）
A．2x2B．1C．2D．$\sqrt{2}$
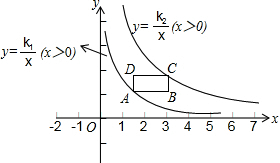19．如图，在平面直角坐标系的第一象限中，有一各边所在直线均平行于坐标轴的矩形ABCD，且点A在反比例函数L1：y=$\frac{{k}_{1}}{x}$（x＞0）的图象上，点C在反比例函数L2：y=$\frac{{k}_{2}}{x}$（x＞0）的图象上．
（1）若点A坐标为（1，1）时，四边形ABCD是边长为1的正方形，则L2的解析式为y=$\frac{4}{x}$（x＞0）．
（2）若点A坐标为（2，2）时，四边形ABCD是边长为1的正方形，则k2=9．
（3）若k1=1，k2=6，且矩形ABCD中平行于x轴的边长为2，平行于y轴的边长为4，写出所有满足条件的C的横坐标不存在．
6．已知有理数：-（-5），-0.25，-|-4|，（-1）2015，2.5，-（-2）3，-52，-$\frac{5}{4}$
（1）分数有-0.25，2.5，-$\frac{5}{4}$，正整数有-（-5），-|-4|，（-1）2015，-（-2）3，-52
（2）求其中所有整数的和．
3．某校初中一年级的男生比女生多32人，其中男生占全年级学生人数的58%，求该校初中一年级共有多少名女生？（根据题意，设未知数，列出方程）
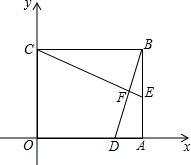2．将一个矩形纸片如图所示放置在平面直角坐标系中，已知OB=5，OC=3，
（1）将纸片沿着CE对折，点B落在x轴上的点D处，求直线CD的解析式；
（2）若CE和BD交于点F，求点F的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网