题目内容
如图，A、B两点的坐标分别为(2,3)、(4,1)．
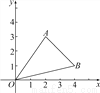
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
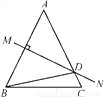
如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是________．
50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．
【解析】
∵MN是AB的垂直平分线，
∴AD=BD，
∴∠A=∠ABD，
∵∠DBC=15°，
∴∠ABC=∠A+15°，
∵AB=AC... 分解因式：①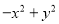
=____________ ；②
=_________________．
；
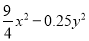【解析】①=y2-x2=（y+x）（y-x）；
②= (9x2-y2)= (3x+y)(3x-y)，
故答案为：①；② . 如图，A、B两点的坐标分别为(2,3)、(4,1)．
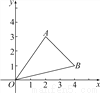
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)． (2012四川雅安)在平面直角坐标系中，三角形ABC的三个顶点坐标分别是A(4，5)，B(1，2)，C(4，2)，将三角形ABC向左平移5个单位后，A点的对应点A′的坐标是( )
A．(0，5)
B．(－1，5)
C．(9，5)
D．(－1，0)
B
【解析】∵三角形ABC向左平移5个单位．∴A(4，5)向左平移了5个单位得到点A′，∴点A′的坐标为(4－5，5)，即A′(－1，5)．故选B． 在平面直角坐标中，△ABC的三个顶点的坐标分别是A(－2,3)，B(－4，－1)，C(2,0)，将△ABC沿x轴方向向左平移_______至△A1B1C1的位置，点A、B、C的对应点分别是A1、B1、C1，使点C1在原点处．
2个单位
【解析】因为C(2,0)沿x轴方向向左平移后对应对应点C1在原点处,即点C沿x轴方向向左平移2个单位,故答案为:2. 已知y关于x的函数：y=（k-2）x2-2（k-1）x+k+1中满足k≤3．
求证：此函数图象与x轴总有交点；
见解析
【解析】试题分析：本题可将函数分成一次函数和二次函数两种情况讨论：当k=2时，函数为一次函数，与x轴一定有交点；当k≠2时，函数为二次函数，让y=0，根据根与系数的关系以及k的取值范围我们可判断出此时的方程是否有解，如果有解，则必与x轴有交点．
试题解析：分两种情况：
（1）当k=2时，函数为y= -2x+3，图象与x轴有交点．
（2）当k≠2时，△=4（k-1）2... 已知抛物线y＝ax2－2x＋1与x轴没有交点，那么该抛物线的顶点所在的象限是( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
D
【解析】∵抛物线y＝ax2－2x＋1与x轴没有交点，
∴△=4-4a＜0，
解得a＞1，
∴抛物线的开口向上，
又∵b=-2，
∴ ＞0，
∴抛物线的对称轴在y轴的右侧，
∴抛物线的顶点在第一象限.
故选D． 等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中，一定是轴对称图形的有（ ）
A. 3个 B. 4个 C. 5个 D. 2个
A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形，是轴对称图形的有3个.
故选：A.