题目内容
已知y关于x的函数:y=(k-2)x2-2(k-1)x+k+1中满足k≤3.
求证:此函数图象与x轴总有交点;
 见解析
【解析】试题分析:本题可将函数分成一次函数和二次函数两种情况讨论:当k=2时,函数为一次函数,与x轴一定有交点;当k≠2时,函数为二次函数,让y=0,根据根与系数的关系以及k的取值范围我们可判断出此时的方程是否有解,如果有解,则必与x轴有交点.
试题解析:分两种情况:
(1)当k=2时,函数为y= -2x+3,图象与x轴有交点.
(2)当k≠2时,△=4(k-1)2...
见解析
【解析】试题分析:本题可将函数分成一次函数和二次函数两种情况讨论:当k=2时,函数为一次函数,与x轴一定有交点;当k≠2时,函数为二次函数,让y=0,根据根与系数的关系以及k的取值范围我们可判断出此时的方程是否有解,如果有解,则必与x轴有交点.
试题解析:分两种情况:
(1)当k=2时,函数为y= -2x+3,图象与x轴有交点.
(2)当k≠2时,△=4(k-1)2...
练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
判断对错:两个会重合的图形一定是中心对称图形; ___________
 错
【解析】两个会重合的图形不一定是中心对称图形,因为还要看是否存在对称中心.
故答案:错.
错
【解析】两个会重合的图形不一定是中心对称图形,因为还要看是否存在对称中心.
故答案:错. 一个多项式分解因式的结果是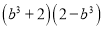 ,那么这个多项式是( )
,那么这个多项式是( )
A. 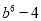 B.
B. 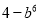 C.
C. 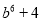 D.
D. 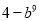
 B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B.
B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B. 如图,A、B两点的坐标分别为(2,3)、(4,1).
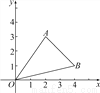
(1)求△ABO的面积;
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′,求△O′A′B′的3个顶点的坐标.
 (1)S△ABO=5;(2)A′(2,0),B′(4,-2),O′(0,-3).
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO=3×4-×3×2-×4×1-×2×2=5,
(2)A′(2,0),B′(4,-2),O′(0,-3).
(1)S△ABO=5;(2)A′(2,0),B′(4,-2),O′(0,-3).
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO=3×4-×3×2-×4×1-×2×2=5,
(2)A′(2,0),B′(4,-2),O′(0,-3). 在平面直角坐标系中,点P(-1,2)向右平移3个单位长度得到的点的坐标是 ______ .
 (2,2).
【解析】试题分析:点P(﹣1,2)向右平移3个单位长度得到的点的坐标是(﹣1+3,2),即(2,2).故答案为:(2,2).
(2,2).
【解析】试题分析:点P(﹣1,2)向右平移3个单位长度得到的点的坐标是(﹣1+3,2),即(2,2).故答案为:(2,2). 抛物线y=2x2+4x+m与x轴只有一个公共点,则m的值为____
 2
【解析】∵抛物线与x轴只有一个公共点,
∴△=0,
∴b2-4ac=42-4×2×m=0;
∴m=2.
故答案为:2.
2
【解析】∵抛物线与x轴只有一个公共点,
∴△=0,
∴b2-4ac=42-4×2×m=0;
∴m=2.
故答案为:2. 已知抛物线y=x2-x-1与x轴的交点为(m,0),则代数式m2-m+2011的值为( )
A. 2009 B. 2012 C. 2011 D. 2010
 B
【解析】∵物线y=x2-x-1与x轴的交点为(m,0),
∴将x=m,y=0代入抛物线解析式得:m2-m-1=0,
∴m2-m=1,
则m2-m+2011=1+2011=2012.
故选:B.
B
【解析】∵物线y=x2-x-1与x轴的交点为(m,0),
∴将x=m,y=0代入抛物线解析式得:m2-m-1=0,
∴m2-m=1,
则m2-m+2011=1+2011=2012.
故选:B. 简便计算:7.292﹣2.712=__.
 45.8
【解析】7.292﹣2.712=(7.29+2.71)(7.29-2.71)=10×4.58=45.8.
45.8
【解析】7.292﹣2.712=(7.29+2.71)(7.29-2.71)=10×4.58=45.8. 用反证法证明命题“对顶角相等”第一步假设__________________.
 对顶角不相等
【解析】试题分析:利用反证法来进行证明时,首先假设结论不成立,即先假设“对顶角不相等”.
对顶角不相等
【解析】试题分析:利用反证法来进行证明时,首先假设结论不成立,即先假设“对顶角不相等”. 
