题目内容
 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.考点:全等三角形的判定
专题:证明题
分析:由∠BAD=∠CAE可得∠CAB=∠EAD,再结合条件可证明△ABC≌△ADE.
解答:证明:∵∠BAD=∠CAE,
∴∠CAE+∠EAB=∠BAD+∠EAB,
即∠CAB=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△DEF(ASA).
∴∠CAE+∠EAB=∠BAD+∠EAB,
即∠CAB=∠EAD,
在△ABC和△ADE中,
|
∴△ABC≌△DEF(ASA).
点评:本题主要考查全等三角形的判定,掌握全等三角形的判定方法,即SSS、SAS、ASA、AAS和HL是解题的关键.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
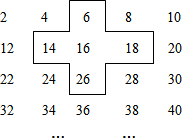 如图,将连续的偶数2,4,6,8,…,排成如下表:
如图,将连续的偶数2,4,6,8,…,排成如下表:
 如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.
如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.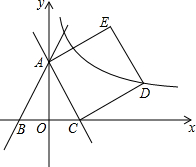 在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=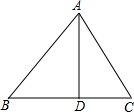 如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是
如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是 如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.
如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.