题目内容
 如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.
如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.考点:全等三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:根据斜边中线等于斜边一半性质即可证明DG=BG,DF=AF,可得∠GDB=∠FDA,即可证明GD⊥DF,进而可以求证△BDG≌△ADF,即可求得DG=DF,即可解题.
解答:解:∵G、F分别是BH和AC的中点,
∴DG=BG,DF=AF,
∴∠GBD=∠GDB,∠FAD=∠FDA,
∵∠C=∠C,AD⊥CD,CE⊥BE,
∴∠CBE=∠CAD,
∴∠GDB=∠FDA,
∵∠GDB+∠GDH=90°,
∴∠ADF+∠GDH=90°,
∴GD⊥DF,
在△BGD和△AFD中,
,
∴△BGD≌△AFD,(ASA)
∴DG=DF.
∴DG与DF之间的关系为DG=DF,DG⊥DF.
∴DG=BG,DF=AF,
∴∠GBD=∠GDB,∠FAD=∠FDA,
∵∠C=∠C,AD⊥CD,CE⊥BE,
∴∠CBE=∠CAD,
∴∠GDB=∠FDA,
∵∠GDB+∠GDH=90°,
∴∠ADF+∠GDH=90°,
∴GD⊥DF,
在△BGD和△AFD中,
|
∴△BGD≌△AFD,(ASA)
∴DG=DF.
∴DG与DF之间的关系为DG=DF,DG⊥DF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BGD≌△AFD是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各组图形中,一定是全等图形的是( )
| A、两个周长相等的等腰三角形 |
| B、两个面积相等的长方形 |
| C、两个斜边相等的直角三角形 |
| D、两个直角边相等的等腰直角三角形 |
二月份的月历,竖着取连续的三个数字,它们的和可能是( )
| A、35 | B、18 | C、72 | D、33 |
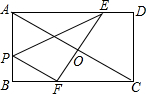 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.