题目内容
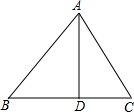 如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是
如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是考点:勾股定理
专题:
分析:先根据AD⊥BC得出△ABD△ACD是直角三角形,再由∠B=45°可知△ABD是等腰直角三角形,故可得出BD的长,进而得出CD的长,根据勾股定理即可得出AC的长.
解答:解:∵AD⊥BC,
∴△ABD△ACD是直角三角形.
∵∠B=45°,
∴△ABD是等腰直角三角形,
∵AD=4,
∴BD=AD=4,
∵BC=7,
∴CD=BC-BD=7-4=3,
∴AC=
=
=5.
故答案为:5.
∴△ABD△ACD是直角三角形.
∵∠B=45°,
∴△ABD是等腰直角三角形,
∵AD=4,
∴BD=AD=4,
∵BC=7,
∴CD=BC-BD=7-4=3,
∴AC=
| AD2+CD2 |
| 42+32 |
故答案为:5.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
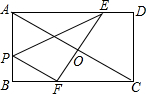 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.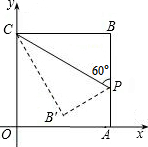 如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-
如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-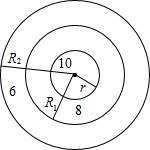 一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm.
一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm. PA,PB切⊙O于点A、B,CD切⊙O于点E.
PA,PB切⊙O于点A、B,CD切⊙O于点E.