题目内容
 如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.
如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.考点:正多边形和圆
专题:证明题
分析:根据多变形的内角和定理得出正五边形的内角和,根据正五边形的各内角相等,可得∠A的度数,根据三角形的内角和定理,可得∠CBD的度数,进而可得出∠ABD的度数,由此可得出结论.
解答:证明:∵五边形ABCDE是正五边形,
∴∠A=∠C=∠ABC=∠EDC=108°,BC=CD,
∴∠CBD=∠CDB=(180°-∠E)÷2=(180°-108°)÷2=36°.
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
∵∠B+∠ABD=108°+72°=180°,
∴AE∥BD.
∴∠A=∠C=∠ABC=∠EDC=108°,BC=CD,
∴∠CBD=∠CDB=(180°-∠E)÷2=(180°-108°)÷2=36°.
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
∵∠B+∠ABD=108°+72°=180°,
∴AE∥BD.
点评:本题考查的是正多边形和圆,熟知正五边形的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有理数a,b在数轴上的对应点的位置如图所示,则( )
有理数a,b在数轴上的对应点的位置如图所示,则( )| A、a+b=0 |
| B、a+b>0 |
| C、a-b<0 |
| D、a-b>0 |
 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.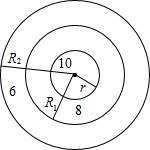 一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm.
一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm. PA,PB切⊙O于点A、B,CD切⊙O于点E.
PA,PB切⊙O于点A、B,CD切⊙O于点E.