题目内容
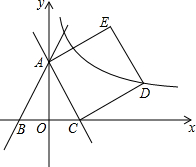 在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)正方形ACDE的AE边的中点是否在上述反比例函数y=
| k |
| x |
考点:反比例函数综合题
专题:综合题
分析:(1)作DH⊥x轴于H,如图,先求出B(-1,0),A(0,2),利用OC=OB得C点坐标为(1,0),再证明△ACO≌△CDH,得到OC=DH=1,CH=OA=2,则可确定D点坐标为(3,1),根据反比例函数图象上点的坐标特征得k=3,所以反比例函数解析式为y=
;
(2)作EG⊥y轴于G,如图,与(1)一样,可证明△ACO≌△EAG,得到OC=AG=1,OA=GE=2,则E点坐标为(2,3),再利用线段中点坐标公式得到AE的中点P的坐标为(1,
),然后根据反比例函数图象上点的坐标特征可判断点P不在反比例函数y=
的图象上.
| 3 |
| x |
(2)作EG⊥y轴于G,如图,与(1)一样,可证明△ACO≌△EAG,得到OC=AG=1,OA=GE=2,则E点坐标为(2,3),再利用线段中点坐标公式得到AE的中点P的坐标为(1,
| 5 |
| 2 |
| 3 |
| x |
解答: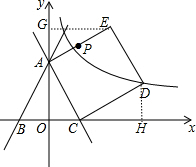 解:(1)作DH⊥x轴于H,如图,
解:(1)作DH⊥x轴于H,如图,
当y=0时,2x+2=0,解得x=-1,则B(-1,0),
当x=0时,y=2x+2=2,则A(0,2),
∵OC=OB,
∴C点坐标为(1,0),
∵四边形ACDE为正方形,
∴∠ACD=90°,AC=CD,
∴∠ACO+∠DCH=90°,
而∠ACO+∠CAO=90°,
∴∠CAO=∠DCH,
在△ACO和△CDH中,
,
∴△ACO≌△CDH(AAS),
∴OC=DH=1,CH=OA=2,
∴OH=OC+CH=1+2=3,
∴D点坐标为(3,1),
∵顶点D恰好在反比例函数y=
(k≠0)的图象上,
∴k=1×3=3,
∴反比例函数解析式为y=
;
(2)正方形ACDE的AE边的中点不在上述反比例函数y=
的图象上.理由如下:
作EG⊥y轴于G,如图,
与(1)一样,可证明△ACO≌△EAG,
∴OC=AG=1,OA=GE=2,
∴OG=OA+AG=2+1=3,
∴E点坐标为(2,3),
而A点坐标为(0,2),
设AE的中点P的坐标为(1,
),
∵1×
≠3,
∴点P不在反比例函数y=
的图象上.
 解:(1)作DH⊥x轴于H,如图,
解:(1)作DH⊥x轴于H,如图,当y=0时,2x+2=0,解得x=-1,则B(-1,0),
当x=0时,y=2x+2=2,则A(0,2),
∵OC=OB,
∴C点坐标为(1,0),
∵四边形ACDE为正方形,
∴∠ACD=90°,AC=CD,
∴∠ACO+∠DCH=90°,
而∠ACO+∠CAO=90°,
∴∠CAO=∠DCH,
在△ACO和△CDH中,
|
∴△ACO≌△CDH(AAS),
∴OC=DH=1,CH=OA=2,
∴OH=OC+CH=1+2=3,
∴D点坐标为(3,1),
∵顶点D恰好在反比例函数y=
| k |
| x |
∴k=1×3=3,
∴反比例函数解析式为y=
| 3 |
| x |
(2)正方形ACDE的AE边的中点不在上述反比例函数y=
| k |
| x |
作EG⊥y轴于G,如图,
与(1)一样,可证明△ACO≌△EAG,
∴OC=AG=1,OA=GE=2,
∴OG=OA+AG=2+1=3,
∴E点坐标为(2,3),
而A点坐标为(0,2),
设AE的中点P的坐标为(1,
| 5 |
| 2 |
∵1×
| 5 |
| 2 |
∴点P不在反比例函数y=
| 3 |
| x |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和正方形的性质;会运用三角形全等的知识解决线段相等的问题;理解坐标与图形性质.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 反比例函数y=
反比例函数y= ”,对于任意实数a,b,都有a
”,对于任意实数a,b,都有a 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE. 如图,一个长方形花坛的长AD为8米,一条对角线AC的长为10米.
如图,一个长方形花坛的长AD为8米,一条对角线AC的长为10米. 如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-
如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-