题目内容
已知抛物线y=ax2-5x+4a过点C(5,4).
(1)求a的值;
(2)求该抛物线顶点的坐标.
(1)求a的值;
(2)求该抛物线顶点的坐标.
考点:二次函数图象上点的坐标特征,二次函数的性质
专题:计算题
分析:(1)根据二次函数图象上点的坐标特征,把C点坐标代入y=ax2-5x+4a中得到关于a的方程,然后解此方程即可;
(2)利用配方法把抛物线解析式配成顶点式即可得到顶点坐标.
(2)利用配方法把抛物线解析式配成顶点式即可得到顶点坐标.
解答:解:(1)把C(5,4)代入y=ax2-5x+4a得25a-25a+4a=4,
解得a=1;
(2)抛物线解析式为y=x2-5x+4
=(x-
)2+
,
所以抛物线的顶点坐标为(
,
).
解得a=1;
(2)抛物线解析式为y=x2-5x+4
=(x-
| 5 |
| 2 |
| 9 |
| 4 |
所以抛物线的顶点坐标为(
| 5 |
| 2 |
| 9 |
| 4 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
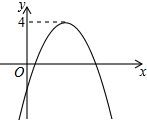 函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )
函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号的实数根 |
| C、有两个相等的实数根 |
| D、没有实数根 |
下列各组图形中,一定是全等图形的是( )
| A、两个周长相等的等腰三角形 |
| B、两个面积相等的长方形 |
| C、两个斜边相等的直角三角形 |
| D、两个直角边相等的等腰直角三角形 |
 反比例函数y=
反比例函数y= 如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.
如图,在△ABC和△ADE中,点E在BC上,∠BAD=∠CAE,∠B=∠D,AB=AD.求证:△ABC≌△ADE.