题目内容
13.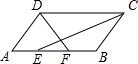 如图,平行四边形ABCD中,AB=5cm,BC=3cm,∠D与∠C的平分线分别交AB于F,E,
如图,平行四边形ABCD中,AB=5cm,BC=3cm,∠D与∠C的平分线分别交AB于F,E,(1)求AE,EF,BF的长;
(2)改变BC的长度,其他条件保持不变,能否使点E,F重合,点E,F重合时,求BC,AE,BE的长.
分析 (1)由平行四边形的性质和平分线可知角之间的等量关系,因此BC=BE=3cm,AE=AF=3cm,求出EF,BF即可;
(2)由AE=BE=BC,AE+BE=AB,即可求得点E、F重合时BC长以及AE的长.
解答 解:(1)∵AB∥CD,
∴∠DCE=∠BEC
又∵∠BCE=∠DCE,
∴∠BEC=∠BCE,
∴BE=BC=3cm,又AB=5cm,
∴AE=2cm.
同理AF=AD=3cm,
∴EF=AF-AE=1cm,
BF=AB-AF=5-3=2(cm);
(2)∵当点E,F重合,由(1)AE=BE,AB=AE+BE,
∴AB=2AE=5cm,
∴AE=BE=2.5cm,
∴BC=BE=2.5cm;
∴点E、F重合时BC长为2.5cm,这时AE的长为2.5cm.
点评 本题考查的是平行四边形的性质以及平行线的性质和等腰三角形的性质等知识,熟练应用等腰三角形的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目