题目内容
8.满足方程组$\left\{\begin{array}{l}{2x-3y=k+1}\\{2x+3y=k}\end{array}\right.$的x,y的值之和为2,求k的值.分析 根据x+y=2,得到y=2-x,代入方程组求出k的值即可.
解答 解:根据题意得:x+y=2,即y=2-x,
代入方程组得:$\left\{\begin{array}{l}{2x-3(2-x)=k+1}\\{2x+3(2-x)=k}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{5x=k+7①}\\{-x=k-6②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{13}{6}}\\{k=\frac{23}{6}}\end{array}\right.$,
则k的值为$\frac{23}{6}$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
18.将抛物线y=2(x+l)2向下平移1个单位长度,再向左平移1个单位长度,平移后抛物线的表达式是( )
| A. | y=2(x+2)2-1 | B. | y=2x2-1 | C. | y=2(x+2)2+1 | D. | y=2(x-1)2-1 |
19.实数x,y满足|2x-y+1|+2$\sqrt{3x-2y+4}$=0,则代数式$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{8}{7}$ | C. | $\frac{5}{3}$ | D. | -$\frac{4}{5}$ |
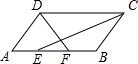 如图,平行四边形ABCD中,AB=5cm,BC=3cm,∠D与∠C的平分线分别交AB于F,E,
如图,平行四边形ABCD中,AB=5cm,BC=3cm,∠D与∠C的平分线分别交AB于F,E,