题目内容
8.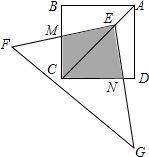 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )| A. | $\frac{5}{9}$a2 | B. | $\frac{4}{9}$a2 | C. | $\frac{2}{3}$a2 | D. | $\frac{1}{4}$a2 |
分析 如图,作辅助线;首先证明四边形EPCQ为正方形;其次求出EP的长度,进而求出正方形EPCQ的面积;证明△PEM≌△QEN,得到S△PEM=S△QEN,进而得到${S}_{重叠部分}={S}_{正方形EPCQ}=\frac{4}{9}{a}^{2}$,即可解决问题.
解答 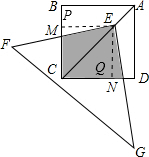 解:如图,过点E作EP⊥BC,EQ⊥CD;
解:如图,过点E作EP⊥BC,EQ⊥CD;
∵四边形ABCD为正方形,
∴∠MCN=90°,CE平分∠MCN,
∴四边形PCQE为矩形,且EP=EQ,
∴四边形PCQE为正方形;
∵EC=2EA,
∴EC:CA=2:3;
∵EP∥AB,
∴△EPC∽△ABC,
∴EP:AB=EC:CA=2:3,
∴EP=$\frac{2}{3}$a,
∴正方形EPCQ的面积为$\frac{4}{9}{a}^{2}$;
∵四边形EPCQ为正方形,
∴∠PEQ=∠MEN=90°,
∴∠PEM=∠QEN;
在△PEM与△QEN中,
$\left\{\begin{array}{l}{∠MPE=∠NQE}\\{PE=NE}\\{∠PEM=∠QEN}\end{array}\right.$,
∴△PEM≌△QEN(ASA),
∴S△PEM=S△QEN,
∴${S}_{重叠部分}={S}_{正方形EPCQ}=\frac{4}{9}{a}^{2}$,
故选B.
点评 该题主要考查了正方形的性质、全等三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用正方形的性质、全等三角形的判定等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
18.比例尺为1:1000的图纸上某区域面积400cm2,则实际面积为( )
| A. | 4×105m2 | B. | 4×104m2 | C. | 1.6×105m2 | D. | 2×104m2 |
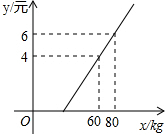 某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围.
某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围. 如图,已知∠α、∠β,用直尺和圆规求作一个∠AOB,使得∠AOB=2∠α-∠β(不写作法,保留作图痕迹).
如图,已知∠α、∠β,用直尺和圆规求作一个∠AOB,使得∠AOB=2∠α-∠β(不写作法,保留作图痕迹).
 如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.
如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.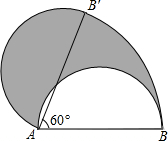 如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积.
如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积.