题目内容
4.为改善南宁市的交通现状,市政府决定修建地铁,甲、乙两工程队承包地铁1号线的某段修建工作,从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍;若由甲队先做20天,剩下的工程再由甲、乙两队合作10天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为15.6万元,乙队每天的施工费用为18.4万元,工程预算的施工费用为500万元,为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,那么工程预算的施工费用是否够用?若不够用,需增加多少万元?
分析 (1)设乙队单独完成这项工程需x天,则甲队单独完成这项工作所需天数是3x天,则甲队的工效为$\frac{1}{3x}$,乙队的工效为$\frac{1}{x}$,由已知得:甲队工作了30天,乙队工作了10天完成,列方程得:$\frac{30}{3x}$+$\frac{10}{x}$=1,解出即可,要检验;
(2)根据(1)中所求得出甲、乙合作需要的天数,进而求出总费用,即可得出答案.
解答 解:(1)设乙队单独完成这项工程需x天,则甲队单独完成这项工作所需天数是3x天,
依题意得:$\frac{30}{3x}$+$\frac{10}{x}$=1,
解得x=20,
检验,当x=20时,3x≠0,
所以原方程的解为x=20.
所以3x=3×20=60(天).
答:乙队单独完成这项工程需20天,则甲队单独完成这项工作所需天数是60天;
(2)设甲、乙两队合作完成这项工程需要y天,
则有y($\frac{1}{20}$+$\frac{1}{60}$)=1,
解得y=15.
需要施工的费用:15×(15.6+18.4)=510(万元).
∵510>500,
∴工程预算的费用不够用,需要追加预算10万元.
点评 本题考查了分式方程的应用,属于工程问题,明确三个量:工作总量、工作效率、工作时间,一般情况下,根据已知设出工作时间,根据题意表示出工效,找等量关系列分式方程,本题表示等量关系的语言叙述为:“甲队先做20天,剩下的工程再由甲、乙两队合作10天完成”.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.为了估计鱼塘中鱼的数量,先捕捉20条鱼给它们分别作上标记,然后放回,待有标记的鱼完全混入鱼群后,第二次捕捉了30条鱼,发现其中3条有标记,从而估计该鱼塘有鱼( )
| A. | 100条 | B. | 200条 | C. | 300条 | D. | 400条 |
19.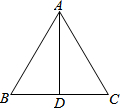 如图,下列条件不能推出△ABC是等腰三角形的是( )
如图,下列条件不能推出△ABC是等腰三角形的是( )
 如图,下列条件不能推出△ABC是等腰三角形的是( )
如图,下列条件不能推出△ABC是等腰三角形的是( )| A. | ∠B=∠C | B. | AD⊥BC,∠BAD=∠CAD | C. | AD⊥BC,∠BAD=∠ACD | D. | AD⊥BC,BD=CD |
9. 有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
 有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a、b在数轴上的位置如图所示,则下列各式正确的是( )| A. | ab>0 | B. | |b|<|a| | C. | b<0<a | D. | a+b>0 |
16. 如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )
如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )
 如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )
如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )| A. | AE=EF=FB | B. | AC=CD=DB | C. | EC=FD | D. | ∠DFB=75° |
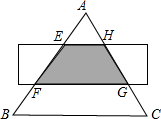 如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.
如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.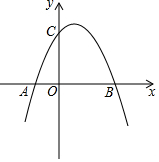 如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.
如图,已知抛物线y=-x2+4x+5与x轴的两个交点为A、B,与y轴交于点C. 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.