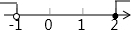题目内容
19.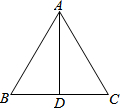 如图,下列条件不能推出△ABC是等腰三角形的是( )
如图,下列条件不能推出△ABC是等腰三角形的是( )| A. | ∠B=∠C | B. | AD⊥BC,∠BAD=∠CAD | C. | AD⊥BC,∠BAD=∠ACD | D. | AD⊥BC,BD=CD |
分析 根据等腰三角形的判定逐项判断即可.
解答 解:
由∠B=∠C可得AB=AC,则△ABC为等腰三角形,故A可以;
由AD⊥BC且∠BAD=∠CAD,可得△BAD≌△CAD,则可得AB=AC,即△ABC为等腰三角形,故B可以;
由AD⊥BC,∠BAD=∠ACD,无法求得AB=AC或AC=BC,故C不可以;
由AD⊥BC,BD=CD,可得AD为线段BC的垂直平分线,可得AB=AC,故D可以;
故选C.
点评 本题主要考查等腰三角形的判定,掌握等角对等边是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
14.在有理数-4,-2,0,3中,大小在-1和2之间的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 3 |
11.己知a=5,|b|=8,且满足a+b<0,则a-b的值为( )
| A. | 13 | B. | -13 | C. | 3 | D. | -3 |
8.下列判断正确的是( )
| A. | 解分式必定产生增根 | |
| B. | 若分式方程的根是零,则必定是增根 | |
| C. | 解分式方程必须验根 | |
| D. | x=3是方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的根 |
9.小明有一块带秒针的手表,随意看一下手表,秒针在3时至4时(包括3时不包括4时)之间的可能性大小为( )
| A. | 1 | B. | $\frac{1}{60}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{12}$ |
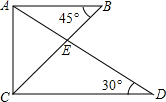 将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$. 如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)
如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)