题目内容
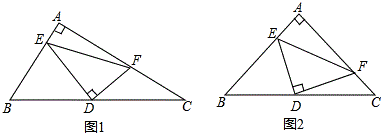
16. 如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )
如图,扇形OAB的圆心角为90°,点C,D是弧AB的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是( )| A. | AE=EF=FB | B. | AC=CD=DB | C. | EC=FD | D. | ∠DFB=75° |
分析 由三角形内角和定理求出∠OCD的度数,根据三角形外角的性质得出∠OEF及∠OFE的度数,由此即可得出结论;根据三角形内角和定理即可得出∠AEO的度数;连接AC,BD,可得出CD=AE=BF,由②可知EF∥CD,所以EF<CD,故可得出结论.
解答 解:∵点C,D是弧AB的三等分点,
∴AC=CD=DB,∴选项B正确;
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∴OE=OF,
∵OC=OD,
∴CE=DF,选项C正确;
连接AC,BD,
∵由选项C知,OC=OD,OE=OF,
∴EF∥CD,
∴EF<CD,
∵C,D是$\widehat{AB}$的三等分点,
∴AC=CD=BD,
∵∠AOC=∠COD,OA=OC=OD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,故选项D正确;
∠OCD=$\frac{180°-30°}{2}$=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴CD=AE=BF≠EF,故选项A错误;
故选A.
点评 本题考查的是圆的综合题,涉及到等腰三角形的性质、全等三角形的判定定理等知识,难度适中.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.己知a=5,|b|=8,且满足a+b<0,则a-b的值为( )
| A. | 13 | B. | -13 | C. | 3 | D. | -3 |
1. 如图,在所标识的角中,互为同旁内角的两个角是( )
如图,在所标识的角中,互为同旁内角的两个角是( )
 如图,在所标识的角中,互为同旁内角的两个角是( )
如图,在所标识的角中,互为同旁内角的两个角是( )| A. | ∠1和∠3 | B. | ∠2和∠3 | C. | ∠1和∠4 | D. | ∠1和∠2 |
8.下列判断正确的是( )
| A. | 解分式必定产生增根 | |
| B. | 若分式方程的根是零,则必定是增根 | |
| C. | 解分式方程必须验根 | |
| D. | x=3是方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的根 |
 如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
如图,甲、乙两人分别从A(1,$\sqrt{3}$),B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向,乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.