题目内容
14.若$\frac{a-b}{a}$=$\frac{2}{5}$,则$\frac{a}{b}$=$\frac{5}{3}$.分析 根据$\frac{a-b}{a}$=$\frac{2}{5}$,应用比例的性质,求出-$\frac{b}{a}$的值是多少,即可求出$\frac{a}{b}$的值是多少.
解答 解:∵$\frac{a-b}{a}$=$\frac{2}{5}$,
∴$\frac{a-b-a}{a}$=$\frac{2-5}{5}$=-$\frac{3}{5}$,
∴-$\frac{b}{a}$=-$\frac{3}{5}$,
∴$\frac{b}{a}$=$\frac{3}{5}$,
∴$\frac{a}{b}$=$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 此题主要考查了比例的性质和应用,要熟练掌握.

练习册系列答案
相关题目
5.在$\frac{1}{x}$,$\frac{m+n}{m}$,$\frac{a{b}^{2}}{5}$,-0.7xy+y3,$\frac{b-c}{5+a}$,$\frac{3{x}^{2}}{π}$中,分式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.小明有一块带秒针的手表,随意看一下手表,秒针在3时至4时(包括3时不包括4时)之间的可能性大小为( )
| A. | 1 | B. | $\frac{1}{60}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{12}$ |
3. 如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
 如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )| A. | 135° | B. | 130° | C. | 120° | D. | 140° |
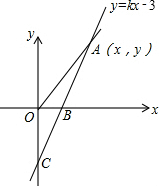 如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别交于B、C两点,且OC=2OB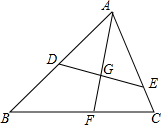 如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.