Question

15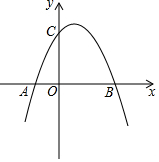．如图，已知抛物线y=-x²+4x+5与x轴的两个交点为A、B，与y轴交于点C．
（1）求A、B、C三点的坐标？
（2）求该二次函数的对称轴和顶点坐标？
（3）若坐标平面内的点M，使得以点M和三点A、B、C为顶点的四边形是平行四边形，求点M的坐标？（直接写出M的坐标）

Answer 1

分析 （1）对应抛物线分别令y=0，x=0解方程即可．
（2）利用配方法即可解决问题．
（3）满足条件的点有三个，设M₁（m，n）．由四边形ABM₁C是平行四边形，推出BC与AM₁互相平分，可得$\frac{-1+m}{2}$=$\frac{0+5}{2}$，$\frac{0+n}{2}$=$\frac{5+0}{2}$，解方程即可解决问题．

解答 解：（1）对应抛物线y=-x²+4x+5，令y=0，得-x²+4x+5=0，解得x=-1或5，
∴A（-1，0），B（5，0），
令x=0得y=5，
∴点C坐标（0，5），
∴A（-1，0），B（5，0），C（0，5）．

（2）∵y=-x²+4x+5=-（x²-4x）+5=-（x-2）²+9，
∴对称轴x=2，顶点坐标为（2，9）．

（3）如图，满足条件的点有三个，设M₁（m，n）．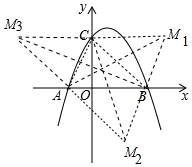

∵四边形ABM₁C是平行四边形，
∴BC与AM₁互相平分，
∴$\frac{-1+m}{2}$=$\frac{0+5}{2}$，$\frac{0+n}{2}$=$\frac{5+0}{2}$，
∴m=6，n=5，
∴M₁（6，5），同理可得M₂（4，-5），M₃（-5，5）．
∴满足条件的点M坐标为（6，5）或（4，-5）或（-5，5）．

点评 本题考查二次函数的综合题、平行四边形的性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用中点坐标公式求点坐标，属于中考常考题型．